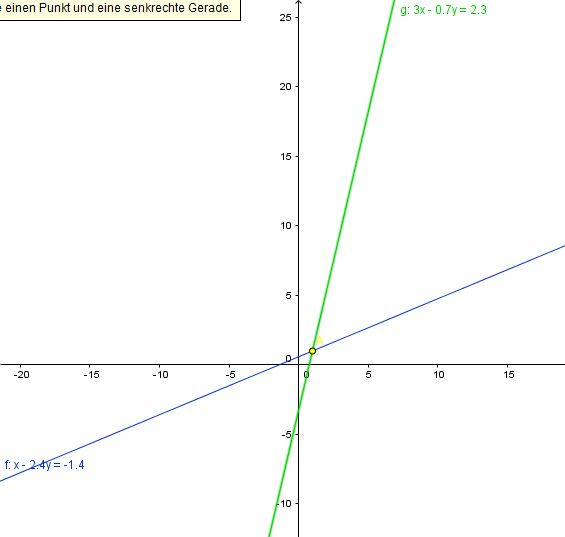
du hast bei solchen Aufgaben in der Regel drei Möglichkeiten, ein Gleichungssystem zu lösen: das Einsetzungs-, das Gleichsetzungs- und das Additionsverfahren. Ich würde in diesem Fall das Einsetzungsverfahren wählen:
Du formst die erste Gleichung nach x um, indem du auf beiden Seiten 2,4y addierst. Daraus ergibt sich
x = 2,4y - 1,4
Das setzt du für x in die zweite Gleichung ein:
3*(2,4y - 1,4) -0,7y = 2,3 Klammer auflösen ergibt
7,2y - 4,2 -0,7 y = 2,3 zusammenfassen
6,5y - 4,2 = 2,3 | +4,2
6,5y = 6,5 | : 6,5
y = 1
Den y-Wert dann in eine der beiden Gleichungen einsetzen, um die x-Koordinate des Schnittpunktes zu erhalten, hier in die zweite Gleichung:
3x - 0,7 * 1 = 2,3
3x - 0,7 = 2,3 |+0,7
3x = 3 | : 3
x = 1
Das Gleichungssystem hat also eine Lösung. Die beiden Geraden schneiden sich in dem Punkt S(1|1)