differenzierbar und gerade Beweis beziehungsweise Gegenbeispiel

Question

Hey:)

Eigentlich sagen ja beide Aussagen das Gleiche aus. Ich hab mir daher folgendes überlegt:

f(x)=f(-x)

Notwendige Bedingung:

f'(x)=0

f"(x)>0 oder f"(x)<0

Nun, man nehme an sei f gerade, aber habe kein Maximum oder Minimum. Dann müsste gelten

f'(x)=0 und ohne VZW das heißt keine Steigung und f"(x)=0.

Da aber immer stetige Funktionen eine Steigung haben, kann die Aussage nicht stimmen.

Comments

Gerade Funktion: f(x) = f(-x)

Einführendes Video zur Symmetrie von Funktionen:

https://www.matheretter.de/wiki/achsensymmetrie https://youtu.be/k3phlEIcd4Q

Dann sollte deine Nachfrage eigentlich erledigt sein. Die Stelle x=0 ist eine spezielle Stelle der Funktion f. 

Answer 1

Hallo Sonnenblume,

zu 1)

Für eine konstante Funktion g mit g(x) = c  ist jede Stelle x sowohl lokale Minimum-  als auch lokale Maximumstelle. Sei also im Folgenden f in keinem Teilintervall von ℝ  konstant.   [editiert]

f(x) =_x∈ℝ  f (-x)      →_Kettenregel   f '(x) =_x∈ℝ  - f ' (-x)     →   f '(0) = - f ' (0)

                                      →   2 *  f '(0) = 0  →    f '(0) = 0

Für ε ∈ ℝ⁺  ist  f '(ε) = - f '(-ε)   →  f ' hat einen Vorzeichenwechsel  bei x=0

x = 0 ist also in jedem Fall eine  lokale Extremstelle.

Nachtrag:

Fakename hat inzwischen hier ein Beispiel angegeben, das zeigt, dass 0 keine lokale Extremstelle sein muss. Allerdings hat diese Funktion andere Extremstellen und ist deshalb kein Gegenbeispiel bzgl. Aussage 1)

https://www.mathelounge.de/447283/existiert-f-r-r-diffbar-mit-f-x-f-x-ohne-lokale-extremstelle-in

zu 2)

Gegenbeispiel:

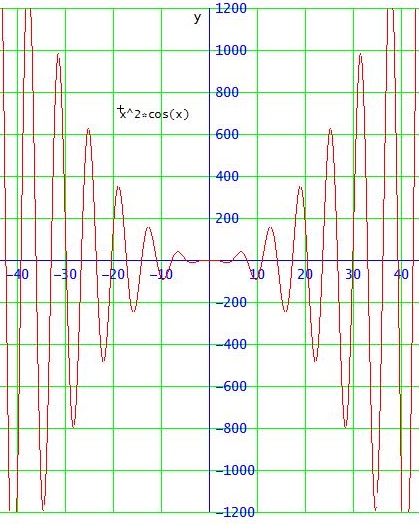
wegen  cos(x) = cos(-x)   ist die Funktion mit  f(x) = x² * cos(x)  gerade und weder nach oben noch nach unten beschränkt, nimmt also weder ein globales Minimum noch ein globales Maximum an,  

denn  lim_{x→ ± ∞}  x² = ∞  und  1 ≤ cos(x) ≤ 1  und  cos(x) wechselt bei x = (k+1) * π/2 mit k∈ℤ  jeweils das Vorzeichen.

Gruß Wolfgang

Comments

Wahrscheinlich eine völlig triviale Frage für dich, aber warum folgt das Fettgedruckte?

Hätte ich da jedes andere x nehmen können?

f(x) =_x∈ℝ  f (-x)      →_Kettenregel   f '(x) =_x∈ℝ  - f ' (-x)     →   f '(0) = - f ' (0) 

---

... Gegenbeispiel angegeben, das wohl auch bei 1) zeigt, dass die Aussage falsch ist.

Das Beispiel zeigt lediglich das, was ich dir schon vor über einer Woche gesagt habe, nämlich dass deine Aussage über den Extremwert bei x=0 falsch ist.

Mit deiner Ansicht, dass damit Aussage 1) widerlegt sei, machst du einen erneuten Fehler.

---

@hj2166

Letzteres war mir inzwischen auch aufgefallen. Das war ein blöder nächtlicher Schnellschuss und meinem en Bedürfnis nach Fehlerkorrektur geschuldet. Habe ich korrigiert.

Du hattest also damals (in der Sache) und hast heute recht. Kannst du die Aussage 1) auch begründen?

(Mir scheint, dass jede Funktion mit den Bedingungen von 1), die in x=0 keine Extremstelle hat, in der Umgebung von x=0 "gedämpft oszillieren" und deshalb andere Extremstellen haben muss. Aber das ist natürlich keine exakte Begründung. )