Hallo Sonnenblume,
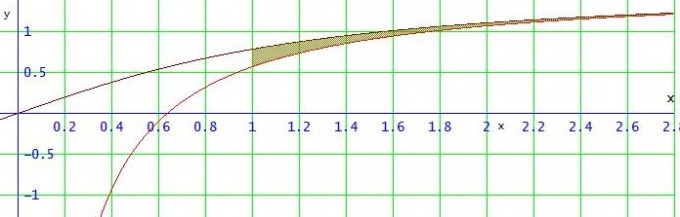
Wenn man davon ausgeht, dass f(x) und g(x) keinen Schnittpunkt haben (vgl. unten #), dann ist der gesuchte Flächeninhalt
1∫∞ (g(x) - f(x)) dx = limz→∞ 1∫z ( arctan(x) - (π/2 - 1/x) ) dx
= limz→∞ 1∫z ( arctan(x) - π/2 + 1/x) ) dx
= limz→∞ [ x·arctan(x) - ln(x2 + 1)/2 - π/2·x + ln(x) ]1z
= limz→∞ [ x·(arctan(x) - π/2) + ln(x) - ln(x2 + 1) / 2 ]1z
= limz→∞ ( z·(arctan(z) - π/2) + ln(z) - ln(z2 + 1) / 2 - ( 1· (π/4 - π/2) + 0 - ln(2)/2 )
=# -1 + 0 + π/4 + ln(2)/2 = ln(2)/2 + π/4 - 1
[ = (ln(4/e4)+π)/4 = ln(√2)+(π/4) -1 , angegeben von Gast2166 bzw. von Simon ]
------------
#
limz→∞ [ z·(arctan(z) - π/2 ] = imz→∞ [ (arctan(z) - π/2) / (1/z) ] = "0/0"
=Hospital limz→∞ [ (1/(z2 + 1)) / ( -1/z2) ] = limz→∞ [ - z2 / (z2 + 1) ] = -1
limz→∞ [ ln(z) - ln(z2 + 1) / 2 ] = limz→∞ [ ( 2 ln(z) - ln(z2 + 1) ) / 2 ]
= limz→∞ [ ( ln(z2 / (z2 + 1) ) / 2 ] = ln(1) / 2 = 0
Der Nachweis f(x) ≠[1,∞[ g(x) ist mir aber bisher nicht gelungen. Lustigerweise berechnen das Näherungsverfahren meines Rechners und das Newtonverfahren tatsächlich Schnittstellen, die sich extrem widersprechen, obwohl die Funktion g(x) - f(x) den Ableitungsterm - 1/(x2·(x2 + 1)) < 0 hat und damit streng monoton fallend ist und deshalb höchstens eine Nullstelle haben könnte. Das liegt daran, dass limx→∞ (g(x) - f(x)) = 0 ist und die Werte dann irgendwann so klein werden, dass sich im Rahmen der Rechengenauigkeit 0 ergibt, was bei verschiedenen Verfahren für unterschiedliche x-Werte der Fall sein kann, auch wenn gar keine Nullstelle vorliegt.
Gruß Wolfgang
Nachtrag:
Auf meine Nachfrage hin hat Ullim dies hier begründet:
https://www.mathelounge.de/454666/arctan-x-%E2%89%A0-%CF%80-2-1-x-in-1-%E2%88%9E
Damit ist die oben im 1.Satz genannte Voraussetzung gezeigt und alles weitere richtig :-)