Hallo Mathlete,
ich finde die Aufgabe interessant, daher nochmal eine ausführliche Antwort.
Du schreibst u.a.: "Tut mir leid, ich weiß einfach nicht weiter :(" Lu hat schon den richtigen Tipp gegeben "Du solltest nun irgendwelche geometrischen Überlegungen anstellen ...". Ich denke da liegt der Schlüssel zum Verständnis der gesamten Aufgabe. IMHO kann jede orthogonale Abbildung als Aneinanderreihung von 2 bzw. 3 Spiegelungen beschrieben werden. Die dritte Spiegelung ist nur notwendig, wenn die Abbildung \(A\) 'links-drehend' ist. Das ist hier aber nicht der Fall, was sich schnell feststellen lässt, wenn man das Kreuzprodukt der ersten beiden Spalten von \(A\) bildet und mit der dritten Spalte vergleicht - also reichen hier 2 Spiegelungen.
Zum weiteren Verständnis betrachte den 2-dimensionalen Fall:
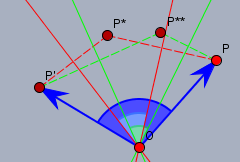
Du siehst dort den Punkt \(P\), der an der roten Achse nach \(P^*\) und von dort an der zweiten roten Achse nach \(P'\) gespiegelt wird. Die Kombination beider Spiegelungen entspricht einer Rotation um den blauen Winkel um den Punkt \(O\), dem Schnittpunkt der beiden roten Achsen. Der blaue Winkel der Rotation ist dabei immer doppelt so groß wie der Schnittwinkel der beiden Achsen. Dabei ist es egal, wie die Achsen liegen, verschiebt man sie in die grüne Position, ist das Zwischenergebnis \(P^{**}\) zwar ein anderes aber das Bild \(P'\) fällt wieder auf den gleichen Punkt wie vorher. Nur der Winkel der Achsen zueinander ist wieder identisch zu vorher.
Im 3-dimensionale wird es etwas schwieriger, da man zunächst die Rotationsachse finden muss. Bei einer linearen Abbildung durch eine orthogonale Rotationsmatrix ist der Drehpunkt in 2D immer der Ursprung (\(O\) im Bild oben). In 3D läuft die Drehachse zwar auch durch den Ursprung, aber ihre genaue Lage muss noch bestimmt werden. Dazu sucht man die sogenannte Fixmenge, d.h. alle Punkte, die durch die Transformation nicht verändert werden. Das sind bei einer Drehung natürlich alle Punkte auf der Drehachse - also eine Gerade. Sei \(d\) ein Punkt auf der Drehachse, so muss also gelten, dass
$$A \cdot d = d \space \Rightarrow (A-E)\cdot d = 0$$
(\(E\) ist die Einheitsmatrix) \(|A-E|\) muss natürlich =0 sein, da sonst die Gleichung nur die Triviallösung \(d=0\) hat. Das ist übrigens identisch mit der Bestimmung des Eigenvektors (hier \(d\)) für den Eigenwert \(\lambda=1\). Und das hast Du oben auch richtig gemacht. Nur die Lösung muss heißen \(x=z\); \(y=0\). Substituiert man \(t\) für \(x\) so lautet die Geradengleichung der Drehachse \(d\)
$$d(t)=\begin{pmatrix} 1 \\ 0\\ 1 \end{pmatrix} \cdot t$$
Und um das ganze zu veranschaulichen habe ich Dir das in Geoknecht dargestellt:
https://www.matheretter.de/geoservant/de?draw=vektor(0%7C0%7C0%202%7C-2%7C1)%0Apunkt(2%7C-2%7C1%20%22X%22)%0Avektor(0%7C0%7C0%202%7C1%7C-2)%0Apunkt(2%7C1%7C-2%20%22Y%22)%0Avektor(0%7C0%7C0%201%7C2%7C2)%0Apunkt(1%7C2%7C2%20%22Z%22)%0Agerade(0%7C0%7C0%201%7C0%7C1)%7B0FF%7D
Die hellblaue Gerade ist die Rotationsachse und die drei Vektoren X, Y und Z sind das durch \(A\) transformierte - also gedrehte - Koordinatensystem.
Jetzt bleibt noch zwei Spiegelebenen zu finden. Man könnte natürlich den Drehwinkel berechnen und dann zwei beliebige Ebenen wählen, deren Schnittgerade =\(d\) ist, und deren Schnittwinkel gleich dem halben Drehwinkel ist. In Deinem Script heißt es aber "Dann bestimmt man W:=(R(f(v)-v))orthogonal und U:=(Rv)orthogonal sowie die Spiegelungen s_W und s_U mit Fix(s_W)=W und Fix(s_U)=U." Dazu betrachten wir wieder den 2-dimensional Fall:
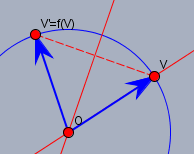
Man wählt einen Punkt \(V\), der nicht auf der Drehachse liegt (hier in 2D heißt das: \(V\ne O\)) und legt die erste Spiegelachse durch \(OV\). Und dann bestimmt man den Differenzvektor \(f(V)-V\) und legt die zweite Spiegelachse senkrecht zu diesem Vektor und durch \(O\). So haben wir auf einfache Weise zwei Spiegelachsen gefunden, deren Verknüpfung die gewünschte Drehung ergibt.
Das ganze gilt es jetzt auf unseren Fall in 3D zu übertragen. Dazu wähle ich \(V=(0;1;0)\) Die Ebene \(U\), die \(d\) und \(V\) enthält, ist
$$U: \space \frac{1}{2} \sqrt{2}\begin{pmatrix} -1 \\0 \\ 1\end{pmatrix} \cdot \vec{x}=0; \quad \text{folgt aus:} \space d \times V=\begin{pmatrix} -1 \\0 \\ 1\end{pmatrix}$$
Für \(W\) ist \(f(V)-V\) bereits der Normalenvektor der gesuchten Ebene
$$f(V)-V=A \cdot V - V=\frac{2}{3}\begin{pmatrix} 1 \\-1 \\ -1\end{pmatrix}$$
demnach gilt
$$W: \space \frac{1}{3} \sqrt{3}\begin{pmatrix} 1 \\-1 \\ -1\end{pmatrix} \cdot \vec{x} = 0$$
Die Matrizen für die zugehörigen Abbildungen \(s_W \rightarrow x'=A_W \cdot x\) und \(s_U \rightarrow x'=A_U \cdot x\) sind
$$A_W=\frac{1}{3}\begin{pmatrix} 1 & 2 & 2\\ 2 & 1 & -2 \\ 2 &-2 &1\end{pmatrix}$$
$$A_U=\begin{pmatrix} 0 & 0 & 1\\ 0 & 1 & 0 \\ 1 &0 &0\end{pmatrix}$$
mit \(A=A_W \cdot A_U\). Falls Du dazu noch Fragen hast, so melde Dich bitte.
Gruß Werner