Hiho! :-)
Vielleicht mal etwas Anschauliches: :-O
|z-1+2i| = |z+3-i|
Wir schreiben die Beträge so um, dass sie Differenzen enthalten
|z - (1-2i)| = |z - (-3 + i)|
Die Beträge lassen sich als Abstände(*) interpretieren:
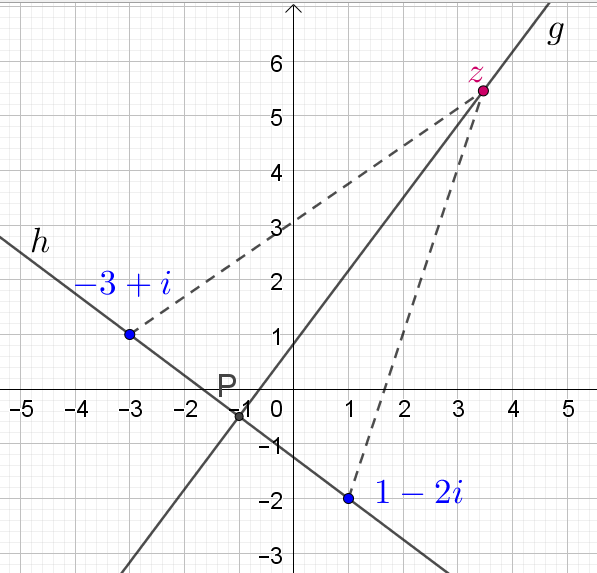
Gesucht ist die Menge aller z, deren Abstände von 1-2i und von -3+i gleich sind. Das sind die Zahlen z, die auf der Mittelsenkrechten g der Strecke von 1-2i nach -3+i liegen. (Guckst du Bild.)
Wir definieren der einfacheren Schreibselei wegen x als den Realteil und y als den Imaginärteil einer komplexen Zahl:
x := Re(z)
y := Im(z)
Mit Hilfe der Geraden h: y = -0,75x - 1,25 und des Punktes P bekommen wir die Gerade g: y = 4/3x + 5/6.
Auf der Geraden g liegen alle z, die der Gleichung |z-1+2i| = |z+3-i| genügen.
Haben fertig L = {z = x + y i | y = 4 / 3 x + 5 / 6}
(Vgl. Antwort von Grossesplüschtier(SCNR): b = 1/6(8a +5) = 4/3 a + 5/6 kann man als Menge schreiben ==> L = {z=a+bi | b = 4/3 a + 5/6}
Bsp.: DIe komplexe Zahl z hat zu -3 + i sowie zu 1 - 2i den gleichen Abstand.
(*) (vgl. Definition Abstand bzw. Summe/Differenz von Vektoren)
Beste Grüße