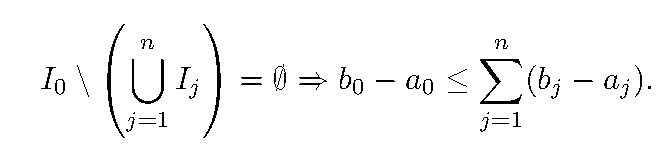
Obiges soll mittels vollständiger Induktion gezeigt werden:
Folgendes ist bekannt: Es geht um Mengentopologie. Seien Ij ⊂ ℝ Intervalle mit Ij = [aj, bj] mit j= 0,...,n
Ich sitze schon den ganzen Tag daran und bekomme es einfach nicht geknackt.
Kann jemand von Euch helfen. Ich bin für jeden Lösungsvorschlag, Tipp, Hinweis, etc sehr dankbar.