Fouriertransformierte von ex^2/2

Question

Jo,

wenn es um Fourier geht, bekommt man eigentlich selten antworten, aber es ist wirklich wichtig diesmal... 

Die Lösung ist wie folgt, wenn da kein Fehler ist... 

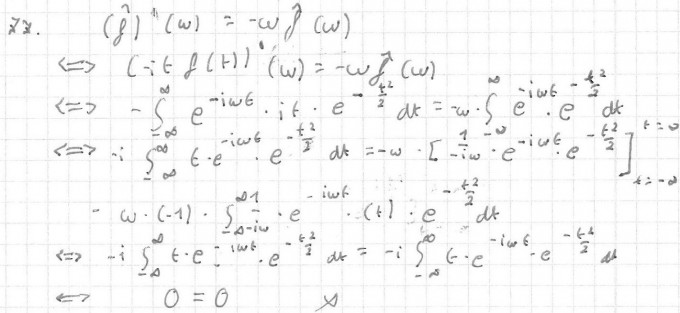
Also meine Frage ist... wie kommt man auf das folgende (3. Zeile), denn der Rest ist dann klar, wenn ich das irgendwie herausfinden kann... 

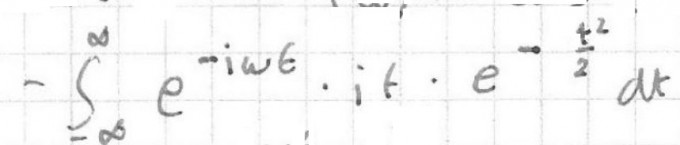
mfg

Answer 1

Hi,
es gilt $$\mathcal{F}\{ f(t) \}(\omega) = \hat f(\omega) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^\infty f(t) e^{-i \omega t } dt$$
Daraus folgt $$\hat f'(\omega) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^\infty (-i t) f(t) e^{-i \omega t } dt$$
mit $f(t) = e^{-\frac{t^2}{2}}$ folgt
$$\hat f'(\omega) = \frac{i}{\sqrt{2\pi}} \int_{-\infty}^\infty \left( -t e^{-\frac{t^2}{2}} \right) e^{-i \omega t } dt$$
Weil $\frac{d}{dt} e^{-\frac{t^2}{2}} = -t e^{-\frac{t^2}{2}}$ gilt folgt mit partieller Integration
$$\hat f'(\omega) = \frac{i}{\sqrt{2\pi}} \int_{-\infty}^\infty \left( \frac{d}{dt} e^{-\frac{t^2}{2}} \right) e^{-i \omega t } dt = \frac{i}{\sqrt{2\pi}} \left[ e^{-\frac{t^2}{2}} e^{-i \omega t } \Bigg|_{-\infty}^\infty - \int_{-\infty}^\infty e^{-\frac{t^2}{2}} (-i \omega) e^{-i \omega t } dt \right] = -\omega \hat f(\omega)$$

Comments

danke für die detaillierte Antwort... aber ich habe noch eine frage.

wie kommt man in der letzten Zeile auf = -w f^w?... egal was ich mache oder wie ich umforme ich komme nicht drauf

mfg

---

* -w f_dach (w)

---

Also meine Rechnung sieht soweit so aus... es fehlt ein t (hier blau) und ein i ist zu viel am ende (rot) :/

mfg

---

es ist schon e^-iwt gemeint, hab nur das minus vergessen 

---

Hi,
der erste Term in der eckigen Klammer ist Null, weil $e^{-\frac{t^2}{2}}$Null ist für $t \to \pm \infty$
Bei dem Integral kann $-i \omega$ vor das Integral ziehen da ja über $t$ integriert wird. Zusammen mit dem Minus vor dem Integral und dem Faktor vor der eckigen Klammer ergibt sich das Ergebnis, wegen $i^2 \omega = -\omega$

---

ok also die linke seite habe ich jetzt hinbekommen... die rechte Seite ist noch unklar :/

ich habs hier rotmarkiert:

mfg

---

Meiner Meinung nach brauchst Du keine rechte Seite. Der Beweis, den ich Dir geschrieben habe, benötigt das nicht. Da wird direkt aus der Definition der Fouriertransformation die Gleichung $\hat f'(\omega) = - \omega \hat f(\omega)$ hergeleitet. Auch den Hinweis braucht man nicht. Du kannst Dir das Leben damit einfacher machen.

---

ja das macht sinn... aber ich glaube mein problem ist was anderes... 

ist das $$\hat f$$ oder mit "·(iw)" noch im integral?

$$\hat f = \int _{ -\infty }^{ \infty }{ { e }^{ -t²/2 } } { e }^{ -iwt }dt$$  

denn ohne *iw im integral kommt man ja auf die Lösung... 

mfg

---

Das $i \omega$ kann man aus dem Integral rausziehen, da ja über $t$ integriert wird.

---

ich meine die rechte seite, wo du meintest, dass es egal ist... links ist mir klar... aber rechts kommt -w(iw) raus 

und das ist -iw² 

und das führt zu -w != -iw²...

ich muss ja zeigen das f_dach'(w) = -w·f_dach ist... 

habe ich also rechts vielleicht mit dem falschen f_dach gearbeitet... sollte das iw rechts nicht das sein?...

---

welches ist richtig:

$$\hat { f } =\int _{ -\infty }^{ \infty }{ { e }^{ -t²/2 } } \cdot (iw){ e }^{ -iwt }dt$$

oder

$$\hat f = \int _{ -\infty }^{ \infty }{ { e }^{ -t²/2 } } { e }^{ -iwt }dt$$

mfg

---

Weder noch. Es gilt $$\hat f(\omega) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^\infty e^{-\frac{t^2}{2}} e^{-i \omega t } dt$$