Ich war neugierig über diese Aufgabe und bin auf folgendes Ergebnis gekommen:
So würde der Rest aussehen.
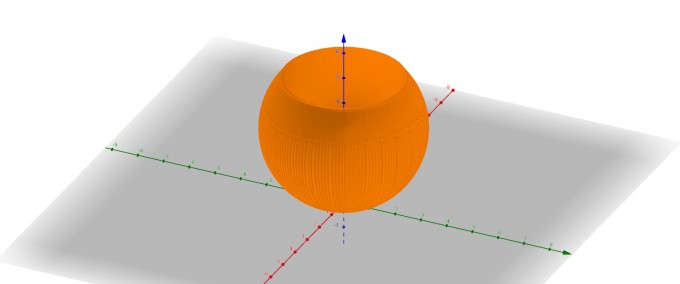
Und hier mit dem Paraboloiden(blau) und der Kugel(rot).
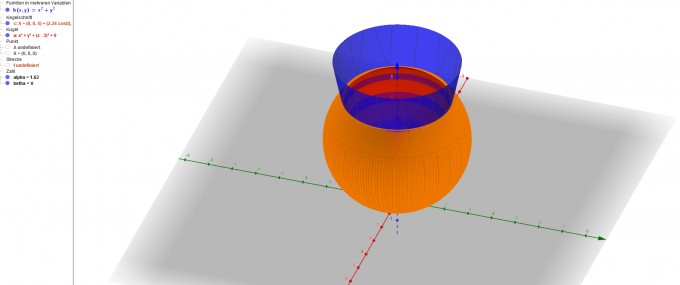
Wie ich vorgegangen bin.
Paraboloid in Koordinatenform:
$$ z=x^2+y^2 $$
Parameterform:
$$ \vec{f}=\begin{pmatrix}r\cdot cos(\phi)\\r\cdot sin(\phi) \\ r^2 \end{pmatrix} $$
Kugelkoordinaten:
$$ \vec{k}=\begin{pmatrix}r\cdot sin(\theta)\cdot cos(\phi)\\r\cdot sin(\theta)\cdot sin(\phi) \\ r\cdot cos(\theta) \end{pmatrix} $$
Ein Querschnitt
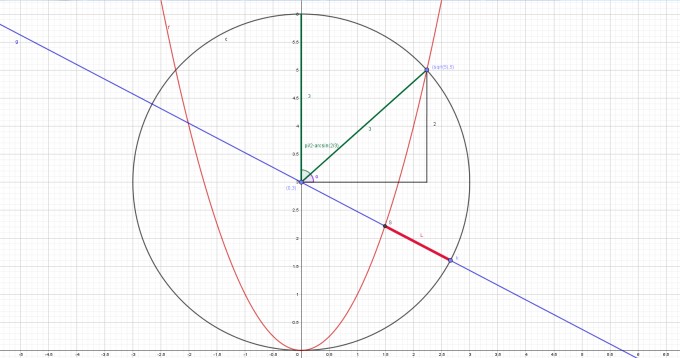
Daraus kann man eine Geradengleichung aufstellen, die durch den Mittelpunkt der Kugel geht:
$$ g:\vec{x}=\begin{pmatrix}0\\0\\3 \end{pmatrix}+\lambda \cdot \vec{k}$$
Damit will ich nun nur noch das Stück der rosanen Strecke bestimmen, genannt L, die immer zwischen Kugel und Paraboloiden liegt. Als Stützvektor wähle ich den Schnittpunkt der Geraden g mit dem Paraboloiden. Dafür wird g mit dem Ortvektor des Paraboloiden gleichgesetzt:
$$ \begin{pmatrix}0\\0\\3 \end{pmatrix}+\lambda \cdot \begin{pmatrix}r\cdot \sin(\theta)\cdot \cos(\phi)\\r\cdot \sin(\theta)\cdot \sin(\phi) \\ r\cdot \cos(\theta) \end{pmatrix}=\begin{pmatrix}r\cdot \cos(\phi)\\r\cdot \sin(\phi) \\ r^2 \end{pmatrix} $$
Dann hat man:
$$\begin{aligned}&i\quad r\cdot \sin(\theta)\cos(\phi)\cdot \lambda\quad&&=r\cdot \cos(\phi) \\&ii \quad r\cdot \sin(\theta)\cdot \sin(\phi)\cdot \lambda&&=r\cdot \sin(\phi) \\ &iii \quad 3+r\cdot \cos(\theta)\cdot\lambda \quad &&=r^2 \end{aligned}$$
$$ \lambda=\frac{1}{sin(\theta)}. $$
Damit lässt sich mit iii r berechnen:
$$ 3+r\cdot\frac{cos(\theta)}{sin(\theta)}=r^2 \Rightarrow r=\frac{cot(\theta)+\sqrt{cot^2(\theta)+12}}{2}. $$
Nun muss der genaue Definitionsbereich für den Winkel θ gefunden werden. Aus der dritten Zeichnung ergibt sich dann:
$$ sin(\alpha)=\frac{2}{3} \Leftrightarrow \alpha=arcsin(\frac{2}{3}) \Rightarrow \beta=\frac{\pi}{2}-\alpha=\underline{\frac{\pi}{2}-arcsin(\frac{2}{3})}. $$
Also gilt nun insgesamt:
$$ \theta \in\Bigg[\frac{\pi}{2}-arcsin(\frac{2}{3}),\pi\Bigg] , \quad \phi\in]0,2\pi ] .$$
Jetzt bestimme ich das Stück rosane Strecke L, in Form einer Geraden mit neuem Richungsvektor, bestehend aus dem Ortsvektor vom Paraboloiden und der Kugel mit dem Mittelpunkt (0,0,3) und Radius r=3:
$$ L:\vec{x}=\begin{pmatrix}r\cdot cos(\phi)\\r\cdot sin(\phi) \\ r^2 \end{pmatrix}+\omega\cdot\ \begin{pmatrix} 3\cdot sin(\theta)\cdot cos(\phi)-r\cdot cos(\phi)\\3\cdot sin(\theta)\cdot sin(\phi)-r\cdot sin(\phi) \\ 3\cdot cos(\theta)+3-r^2\end{pmatrix} , \quad \omega \in [0,1].$$
Insgesamt hat man als Menge M also:
$$ M:=\Bigg\{\begin{pmatrix}x\\y\\z \end{pmatrix}\in \mathbb{R^3}: \begin{pmatrix}x\\y\\z \end{pmatrix}=\begin{pmatrix}r\cdot cos(\phi)\\r\cdot sin(\phi) \\ r^2 \end{pmatrix}+\omega\cdot\ \begin{pmatrix} 3\cdot sin(\theta)\cdot cos(\phi)-r\cdot cos(\phi)\\3\cdot sin(\theta)\cdot sin(\phi)-r\cdot sin(\phi) \\ 3\cdot cos(\theta)+3-r^2\end{pmatrix}, \quad \omega \in [0,1],\quad\theta \in\Bigg[\frac{\pi}{2}-arcsin(\frac{2}{3}),\pi\Bigg] , \quad \phi\in]0,2\pi ], \\ r=\frac{cot(\theta)+\sqrt{cot^2(\theta)+12}}{2}\Bigg\}. $$
Menge_M.ggb (21 kb)