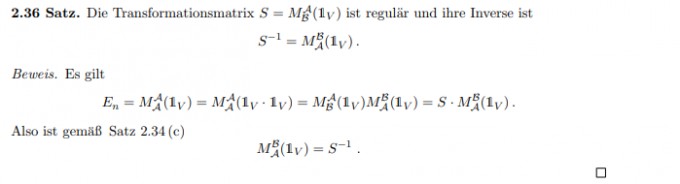
Ich habe Probleme einen Beweis aus meinem Skript zu verstehen. (siehe Bild) $$ M^{ A }_A (1_v*1_v)=M^{ B }_A (1_v)*M^{ A }_B (1_v)$$ Um auf den ersten Teil dieser Gleichung zu kommen wird ja einfach nur benutzt, dass die Identitätsabbildung nacheinander ausgeführt das Gleiche wie die Identitätsabbildung ist. Nur verstehe ich den nächsten Schritt nicht wirklich. Könnte mir jemand erklären was genau hier wie benutzt wird?
Grüße,
planlos