Hallo Catwoman,
es kommt natürlich darauf an, wie Deine Frage
Wie kann ich den graph bestimmen von dieser funktion
gemeint ist! Wir hatten das zunächst so verstanden, dass Du den Graphen der Funktion \(f(x)=1,5\sqrt{x-0,5}\) suchst. Dann ist das Aufstellen der Wertetabelle und Eintragen in ein Koordinatensystem (mit oder ohne Computer) der richtige Weg.
Wenn das aber so gemeint ist, dass Du aus drei (oder mehr) vorgegebenen Graphen den passenden bestimmen sollst, dann sind die beiden bisherigen Antworten zumindest unvollständig.
Zumal wenn Du schreibst:
wie kann ich dann bestimmen welche es ist, ohne eine Wertetabelle zu machen
Dazu muss man wissen, dass die Wurzelfunktion eine liegende Parabel ist. Da ändert auch der Faktor 1,5 und die Verschiebung um 0,5 nichts daran. Eine Parabel hat keine Asymptote, damit scheidet der erste der drei Graphen bereits aus. Und jede Parabel wächst quadratisch in Richtung Ihrer Öffnung. Dazu ein Bild:
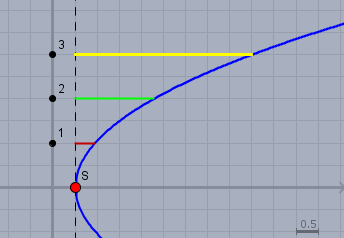
Vom Scheitelpunkt \(S\) der Parabel denkt man sich eine senkrechte Gerade (die schwarze gestrichelte Linie im Bild). Dann geht man eine Einheit nach oben und schaut nach wie weit die Parabel nun von der Senkrechten entfernt ist. Das ist die rote Strecke. Das ist hier etwas weniger als ein Kästchen. Bei zwei Einheiten nach oben schaut man wieder nach; das ist die grüne Strecke. Wenn es sich um eine Parabel handelt muss die grüne Strecke \(2^2=\) viermal so lang sein, wie die rote. Hier sind es knapp vier Kästchen; das passt also. Verdreifacht man den Weg nach oben, so muss der Abstand zur Parabel (dle gelbe Strecke) das \(3^2=\) neunfache betragen.
Diese Eigenschaft ist nur beim rechten der drei Graphen gegeben. Und das kann man ganz ohne Wertetabelle sehen. Versuche das gleiche mal beim mittleren Graphen; Du wirst sehen, dass sich der Streckenzuwachs dort deutlich anders verhält.
Gruß Werner