Kreis der den Kreis K und die Gerade g berührt bestimmen. Nur noch der Radius fehlt !

Question

Aufgabe

Gegeben sind der Kreis K mit dem Mittelpunkt (20I0) und dem Radius r = 15 und die Gerade
g: 4x-3y+20 = 0. 
Bestimmen Sie den Mittelpunkt und Radius des kleinsten Kreises, welcher die Gerade g und den Kreis K berührt. 

Ansatz
Kreis ins Koordinatemsystem eingetragen.
Die Orthogonale h zu g gebildet.
---> h(x) = -3/4x + 15

Für den Mittelpunkt des kleineren Kreises: h(x) = g(x) 
--->  x = 4, y = 15
    ---> M2(4I15)

K2: (x-4)² + (y-15)² = r²

Frage: Wie finde ich den Radius heraus ? 

Answer 1

mach es doch so:

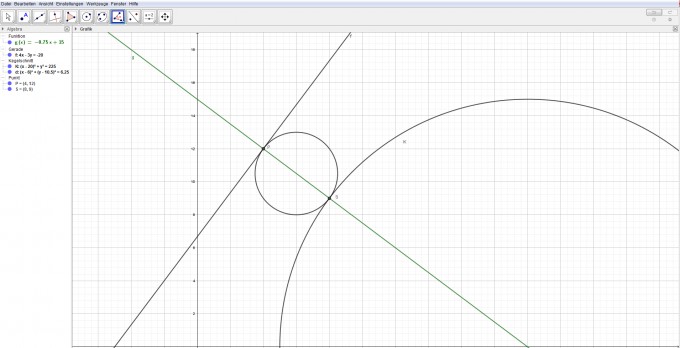
Orthogonale zu g, die durch den Mittelpunkt M(20|0) geht ist $$ o(x)=-\frac{3}{4}\cdot x+15. $$

Schnittpunkt von g und o berechnen ergibt:

$$ o=g\\-\frac{3}{4}\cdot x+15=\frac{4}{3}\cdot x+\frac{20}{3}\\ \Leftrightarrow x=4\qquad y=12\qquad P(4|12) $$

Schnittpunkt von K und o berechnen ergibt:

$$ y=o(x)=-\frac{3}{4}\cdot x+15\\(x-20)^2+\Big(-\frac{3}{4}\cdot x+15\Big)^2=225\\ \Leftrightarrow 0=x^2-40x+256\\x_{1,2}=20\pm 12\\x_1=32\\x_2=8\\o(32)=-9\\o(8)=9 $$ x_2 ist sinnvoll zu wählen, da der Punkt somit näher an g dran ist. Dann hat man den Schnittpunkt S(8|9).

Abstand von P und S ergibt $$ d(P;S)=\sqrt{(8-4)^2+(9-12)^2}=5 $$ Also muss der Radius r=2,5 sein. Nun der Mittelpunkt der Strecke PS:

$$ N\Bigg(\frac{8+4}{2} \Bigg|\frac{9+12}{2} \Bigg)=N(6|10,5) $$

Damit hat man diesen Kreis:

$$ K_{min}:(x-6)^2+(y-10,5)^2=2,5^2 $$

Comments

Super Antwort ! 

Vielen Dank !

---

Kein Problem :)

Answer 2

Hallo

der Mittelpunkt liegt doch auf der Mitte der Schnittpunktes von h mit dem Kreis  und der Geraden g. also M=(6,10.5) der Radius ist dann der Abstand zwischen dem Schnittpunkt und dem Mittelpunkt. Da der Kreis ja g berühren soll. kann sein M nicht auf g liegen, da ist dein Fehler. hier die berichtigte Zeichnung. zur Kontrolle r=2,5