Hallo limonade,
Der von lul vorgeschlagene Weg ist richtig, mündet aber in einer üblen Rechnerei. Setzt man alle Werte in das Skalarprodukt ein, so erhält man wegen der Wurzelausdrücke nach dem Quadrieren schließlich: $$y^4-6y^3-8y^2+30y-17 = 0$$ (wenn man sich nicht verrechnet hat!) Klar, mit ein wenig Erfahrung lässt sich eine Nullstelle \(y_0=1\) raten, was einen nach der Polynomdivision weiter bringt.
Alternativ kann man sich die geometrische Konstruktion anschauen. Alle Punkte, von denen aus \(A\) und \(B\) in einem Winkel von \(45°\) erscheinen, liegen auf einem sogenannten Fasskreisbogen.
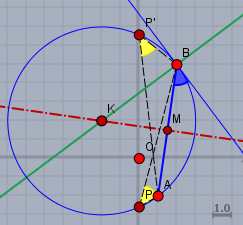
Der Mittelpunkt \(K\) dieses Fasskreisbogens (was ein Kreisbogen ist), ist der Schnittpunkt der Orthogonalen (grün) auf dem Schenkel, der unter \(45°\) an der Strecke \(AB\) anliegt, und der Mittelsenkrechten (rot) der Strecke \(AB\). Das Dreieck \(\triangle BKM\) ist immer ein rechtwinkliges und in diesem Fall auch ein gleichschenkliges Dreieck. Damit kann man den Vektor \(\vec{MK}\) und danach \(K\) leicht aus \(AB\) bzw. \(MB\) bestimmen: $$\vec{MB} = \begin{pmatrix} 0,5\\ 3,5\end{pmatrix} \quad \Rightarrow \vec{MK} = \begin{pmatrix} -3,5\\ 0,5\end{pmatrix}$$ $$K= M + \vec{MK} = \begin{pmatrix} 1,5\\ 1,5\end{pmatrix} + \begin{pmatrix} -3,5\\ 0,5\end{pmatrix} = \begin{pmatrix} -2\\ 2\end{pmatrix}$$ Der Radius des Fasskreisbogens ist \(|KB|=5\) woraus zusammen mit \(K\) sofort die Kreisgleichung folgt: $$(x+2)^2+(y-2)^2=25$$ Jetzt nur noch \(x=0\) einsetzen (\(P\) liegt auf der Y-Achse) $$(y-2)^2=25-4=21$$ und man braucht noch nicht mal die pq-Formel. Die Lösung für die beiden Y-Koordinaten von \(P\) (und \(P'\)) fällt einem sofort in den Schoss: $$y_{1,2}=2\pm \sqrt{21}$$ Vorteil hier: man kann jedes Zwischenergebnis sofort graphisch überprüfen. Das kannst Du bei dem Weg über das Skalarprodukt nicht ohne weiteres.