Frage zu Least Median Square

Question

Bräuchte Hilfe bei einer Frage. Könnte mir jemand helfen ?

Kann mir jemand den Algorithmus Least Median of Square am Bespiel einer Geradenschätzung beschreiben ?

Comments

Kannst du mal versuchen die Fachbegriffe in korrekte deutschsprache mathematische Begriffe zu übersetzen?

---

Ja - das 'Median' in 'Least Median Square' hatte mich stutzig gemacht, aber IMHO ist wohl nur die klassische 'Methode der kleinsten Quadrate' gemeint.

@Alpay: bis wann brauchst Du eine Antwort? Ist das eine Schulaufgabe/-Arbeit oder geht es Dir rein um das Verständnis?

---

Es geht mir rein um das verständnis und wie das dargestellt sein sollte. Also theoretisch eine Aufgabe

---

Wikipedia verlinkt

https://en.wikipedia.org/wiki/Least_squares mit https://de.wikipedia.org/wiki/Methode_der_kleinsten_Quadrate

Da bleibt die Frage, was du mit "Median" machen sollst? Hast du eine exakte Definition der Methode, die man dir erklären soll?

Median: Vgl. https://en.wikipedia.org/wiki/Median

---

Nein. Habe keine Defintion leider.

---

Vom Duplikat:

Titel: Least of Median Statistik Frage

Stichworte: median,algorithmus,statistik,arithmetisches

 

Der Least Median of Squares ist ein robuster Algorithmus zur Bestimmung einer ,,

halbwegs wahrscheinlichen Lösung" eines Ausgleichungsproblems.

Beschreiben am Beispiel einer Geradenschätzung.

Könnte mir bitte jemand hierbei helfen am Beispiel komme ich nicht so richtig weit.

Answer 1

Hallo Alpay,

ich versuche mal eine Erklärung: Mal angenommen, Du hast drei Paare $(x_i;\, y_i)$ $$\begin{array}{cc} x_i & y_i \\ \hline 2 & 9,1 \\ 3 & 9,3 \\ 4 & 10,1 \end{array}$$ und suchst jetzt eine Gerade - bzw. lineare Funktion, die diese Punkte möglichst gut trifft. Eine lineare Funktion hat die allgemeine Form: $$y(x)=m\cdot x + b$$ Setzt man ein $x_i$ in die Geradengleichung ein, so erhält man $y(x_i)= mx_i + b$. Das Ergebnis ist i.A. nicht $y_i$, sondern zwischen $y_i$ und $y(x_i)$ legt ein Delta: $$\Delta_i = y(x_i) - y_i = mx_i + b - y_i$$ Eine Gerade die die Werte 'möglichst gut' trifft, ist die, bei der die Summe der Quadrate aller Abweichungen $\Delta_i$ möglichst klein sein ist. Also muss folgender Ausdruck minimiert werden:

$$\sum_{i=1}^3 \Delta_i^2 = \sum_{i=1}^3 (mx_i + b - y_i)^2 \, \to \min$$ Um den Extremwert zu bestimmen wird die Summe nach den Variablen - in diesem Fall $m$ und $b$ - abgeleitet und die Ableitungen werden zu 0 gesetzt:

$$\begin{aligned} \frac{\partial \sum}{\partial m} &= \sum_{i=1}^3 2(mx_i + b - y_i) x_i = 0 \\ \frac{\partial \sum}{\partial b} &= \sum_{i=1}^3 2(mx_i + b - y_i) = 0\end{aligned}$$ Damit erhält man zwei Gleichungen nit den zwei Unbekannten $m$ und $b$. Das kann man noch etwas sortieren:

$$\begin{aligned} m \sum_{i=1}^3 x_i^2 + b\sum_{i=1}^3 x_i &= \sum_{i=1}^3 x_iy_i \\ m \sum_{i=1}^3 x_i + 3b &= \sum_{i=1}^3 y_i \end{aligned}$$ Mit den Daten von oben erhält man:

$$\begin{aligned} \sum_{i=1}^3 x_i^2 &= 2^2 +3^2 + 4^2 = 29 \\ \sum_{i=1}^3 x_i &= 2 +3 +4 = 9 \\ \sum_{i=1}^3 x_iy_i &= 2 \cdot 9,1 + 3 \cdot 9,3 + 4 \cdot 10,1 = 86,5 \\ \sum_{i=1}^3 y_i &= 9,1 + 9,3 + 10,1 = 28,5\end{aligned}$$ Einsetzen in das obige Gleichungssystem: $$\begin{aligned} 29 m + 9 b = 86,5 \\ 9 m + 3 b = 28,5 \end{aligned}$$ führt zu der Lösung: $m=\frac12$ und $b=8$. Das ganze nochmal als Graphik:

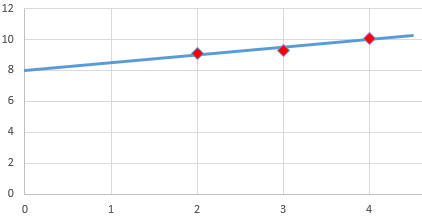
Die roten Punkte sind die $(x_i;\,y_i)$ von oben und die blaue Gerade ist der Graph der Funktion $y=\frac12 x + 8$ .

Frage bitte nach, wenn Du etwas nicht verstanden hast oder Dir eine Information fehlt und sehe Dir bitte auch meine Antwort bei dieser Frage an https://www.mathelounge.de/571304/gezwungene-regressiongerade-durch-….

Gruß Werner

Comments

Hallo Werner,

Wie bist du nochmal auf m= 1/2 und b= 8 gekommen ?

Und die 3b ist es die Hälfte von der 9b in die zweite Gleichung eingebaut ?

Danke

---

Wie bist du nochmal auf m= 1/2 und b= 8 gekommen ?

Das ist die Lösung dieses Gleichungssystem: $$\begin{aligned} 29 m + 9 b = 86,5 \\ 9 m + 3 b = 28,5 \end{aligned}$$Multipliziere die zweite Gleichung mit 3:$$27 m + 9 b = 85,5$$und ziehe sie von der ersten ab:$$2 m + 0 b = 1 \quad \implies m = \frac 12$$dann $m$ in die zweite Gleichung einsetzen:$$9 \cdot \frac 12 + 3 b = 28,5 \quad \implies b=8$$

Und die 3b ist es die Hälfte von der 9b in die zweite Gleichung eingebaut ?

Welche $3b$ meinst Du? aus dieser Gleichung:$9 m + 3 b = 28,5$ oder diese hier $m \sum_{i=1}^3 x_i + 3b = \sum_{i=1}^3 y_i$??

und $3b$ ist auch nicht die Hälfte von $9b$.

---

Ich meinte wie du auf 9m+3b gekommen bist ?

---

Ich meinte wie du auf 9m+3b gekommen bist ?

Das stammt aus der Gleichung da drüber

$$m \textcolor{#00f}{\sum_{i=1}^3 x_i} + 3b = \textcolor{#0a0}{\sum_{i=1}^3 y_i}$$

die wiederum aus der Ableitung nach $b$ folgt. Ich habe eingesetzt:

$$\textcolor{#00f}{\sum_{i=1}^3 x_i} = 9 \\ \textcolor{#0a0}{\sum_{i=1}^3 y_i}= 28,5$$macht:$$m \cdot 9 +3b = 28,5$$

Answer 2

Dann lies einmal das hier: https://de.wikipedia.org/wiki/Methode_der_kleinsten_Quadrate#Beispie…

und dann noch auf Englisch

https://en.wikipedia.org/wiki/Linear_least_squares und dort das Beispiel https://en.wikipedia.org/wiki/Linear_least_squares#Example

Wenn du damit durch bist, am besten kurz melden, wo du aussteigst.

Comments

Ok. Ich lese es nochmal ordentlich aber das Beispiel auf englisch ist die Geradenschätzung oderdie polynomial regression. Ok ich fasse es dann zusammen auf deutsch