Hallo Marx,
die kurze Fassung ist: die Normalgleichung lautet allgemein: \(A^TA\cdot \alpha = y\) In Deinem Fall wird nur ein Wert für die Steigung der Gerade gesucht, folglich besteht hier der Vektor \(\alpha\) nur aus einem Element, aus der Steigung. Der Zusammenhang ist linear, daraus folgt: $$A= \begin{pmatrix} 263,7 & 476,99 & 692,74 & 909,63 & 1120,91 & 1324,96\end{pmatrix}^T$$ und der Y-Vektor ist wie gehabt: $$y = \begin{pmatrix} 26,4 & 52,8 & 79,2 & 105,6 & 132 & 158,4 \end{pmatrix}T$$ Einsetzen in die Normalgleichung gibt: $$4616330,8243 \cdot \alpha = 540902,472 \quad \Rightarrow \alpha \approx 0,1172$$ Eine Skizze zur Verifikation:
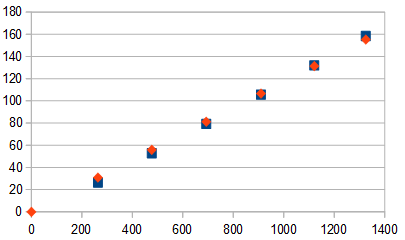
Die blauen Quadrate sind die gegebenen Punkte und die orangen Rauten die Punkte aus der Regressionsrechnung.
Die lange Version: Eine Gerade durch den Ursprung hat die allgemeine Form \(y=mx\). \(m\) ist die Steigung. Existiert ein \(m\), so ist das Delta \(\Delta_i\) gegenüber jedem gegebene Wert \((x_i, \, y_i)\): $$\Delta_i = y_i - m\cdot x_i$$ Das Ziel ist es, die Summe aller Quadrate dieser Abweichungen zu minimieren - also: $$\sum \Delta_i^2 = \sum (y_i - m\cdot x_i)^2\to \min$$ Dazu leitet man die Summe nach \(m\) ab und setzt es zu 0: $$\frac{\partial \sum \Delta_i^2}{\partial m} = \sum 2(y_i - m\cdot x_i)x_i = 0$$ Daraus folgt: $$ \begin{aligned} \sum 2(y_i - m\cdot x_i)x_i &= 0 \\ \sum (y_i - m\cdot x_i)x_i &= 0 \\ \sum y_ix_i - \sum m\cdot x_i^2 &= 0 \\ m \sum x_i^2 &= \sum y_ix_i \\m &= \frac{\sum y_ix_i}{ \sum x_i^2}\end{aligned}$$ Und da $$\sum x_iy_i = A^T \cdot y = 540902,472$$ und $$\sum x_i^2= A^T\cdot A = 4616330,8243$$ ist die Rechnung - und somit auch das Ergebnis - das selbe wie oben: \(m\approx 0,1172\).
Gruß Werner