Zeichnen sie den Graphen der Funktion f(x)=1/2x+3 im Intervall -7<x<1 sowie Graphen spiegeln

Question

Ich habe mal eine Frage, eine ähnliche zum selben Thema wurde gestern schon von einem Kumpel gepostet.

Hier meine Frage bzw. die Aufgabe:

Gegeben ist eine Funktion f durch die Gleichung  y=f(x)=1/2x +3

 

a)Zeichnen sie den Graphen der Funktion mindestens im Intervall -7<x<1 (DAS VERSTEH ICH GARNICHT -.-)

b)Spiegeln sie den Graphen an der y-Achse

c)Das Spiegelbild sei der Graph einer Funktion g

d)Die Graphen schließen mit der x-Achse ein Dreieck ein.

e)Ein anderes Dreieck hat dieselben Eckpunkte auf der x-Achse, als dritten Eckpunkt aber den Punkt P(4;3). Begründen sie,dass beide Dreiecke den gleichen Flächeninhalt haben.

 

Ich sehe wirklich überhaupt nicht durch und hoffe auf eine Antwort :(

Comments

a)Zeichnen Sie den Graphen der Funktion mindestens im Intervall -7<x<1 (DAS VERSTEH ICH GARNICHT -.-)

Deine x-Achse muss links mindestens bei -6.9999999 beginnen und darf frühestens bei + 0.9999999 enden.

Bei der Spiegelung brauchst du allerdings auch alle x- Werte bis etwa 7. Beginn somit links bei etwa - 7 und schau, dass +7 nicht neben dem Blatt liegt.

Answer 1

a) Um den Graphen zu zeichen, suchst du dir einfach zwei Punkte, die auf dem Graphen liegen und verbindest die dann: weil es eine lineare Funktion ist, reicht das völlig.

Mögliche Punkte kriegst du, wenn du für x Zahlen einsetzt und das entsprechende y notierst. Der Punkt ist dann (x, y).

Zum Beispiel:
x = 0: f(0) = 1/2*0 + 3 = 3 ⇒ Ein Punkt ist (0,3)

x = 2: f(2) = 1/2*2 + 3 = 1+3 = 4 ⇒ Ein zweiter Punkt ist (2, 4)

b) Das Bild sieht dann so aus:

 

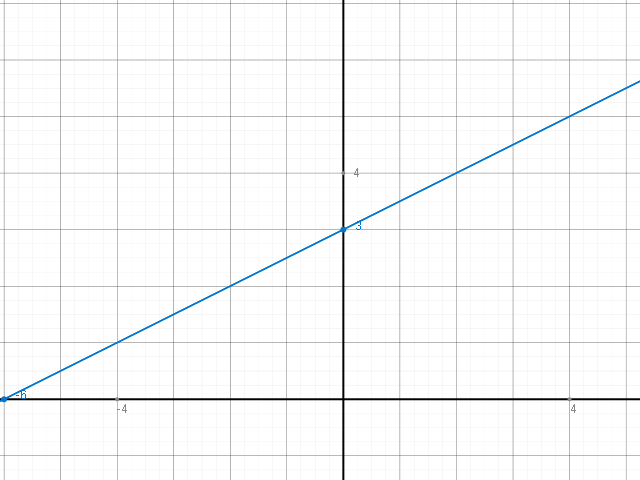
Spiegelt man den Graphen an der y-Achse:

 

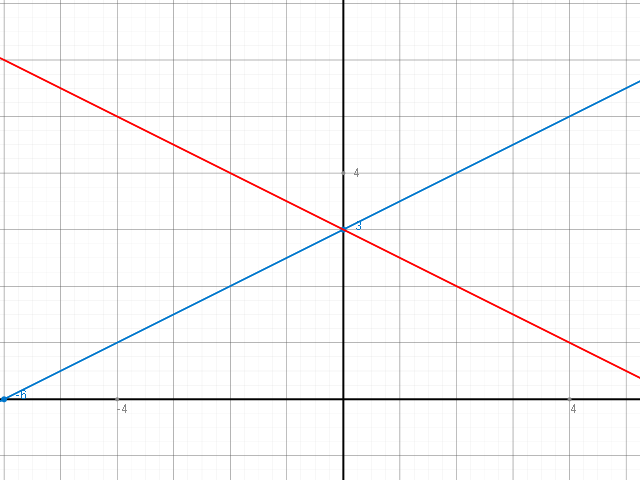
Verschiebt man den spitzen Punkt des Dreiecks nun zu (4, 3) dann verändert sich die Höhe des Dreiecks nicht, die ist nämlich immer noch 3.

Die Grundseite bleibt aber sowieso die gleiche, weil die beiden Punkte beibehalten werden.
Nach der Formel für den Flächeninhalt eines Dreiecks

A = 1/2*g*h

bleibt der Flächeninhalt also gleich!