Nur mal eine Idee: (Ich bitte um eine Bestätigung oder mögliche Korrektur!)
An den Übergangsstellen \(\frac{-pi}{2}\) und \(\frac{pi}{2}\) müssen die Funktionswerte der Teilfunktionen übereinstimmen.
Dann hätte man:
$$ -3*sin(-pi/2)=3 $$
$$ cos(pi/2)+1=1 $$
Damit kann man ein LGS aufstellen
$$ A*sin(-pi/2)+B=3 $$
$$ A*sin(pi/2)+B=1 $$
Die Lösungen sind:
$$ A = -1 $$ und $$ B = 2 $$
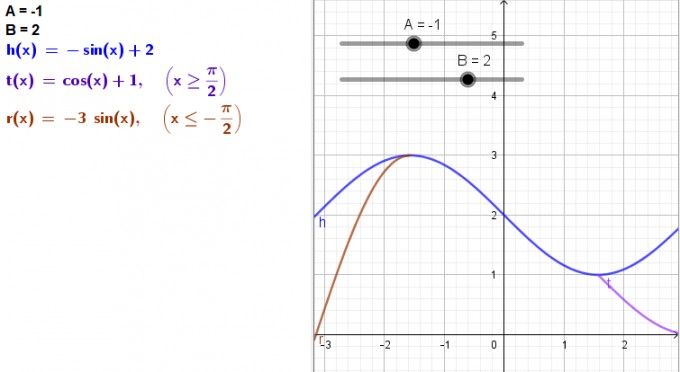
Das sieht dann so aus: