Aufgabe:
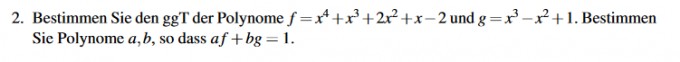
Problem/Ansatz:
Hi, den ggT der beiden Polynome habe ich bereits bestimmt, indem ich beide mit der Polynomdivision dividiert habe und bin schließlich auf 4x2 - 4 = ggT gekommen. Nun verstehe ich den zweiten Teil der Aufgabe nicht richtig, ich muss das Ganze nun in die Form af + bg = 1 bringen. Also den erweiterten Euklidischen Algorithmus anwenden?
1 = a * (x4 + x3 + 2x2 + x - 2 ) + b * (x3 - x2 + 1) also...
Wie komme ich nun auf die gesuchten Variablen a und b, ich muss sicherlich irgendwie den ggT auch dazu verwenden aber ich weiß nicht wo.