Hallo Mathegemeinde,
ich versuche gerade, mir einen sicheren Umgang mit Summen anzueignen.
Nun stehe ich vor der Formel für die geometrische Summe und zusätzlich vor einer weiteren Formel,
welche häufig gebraucht werden.
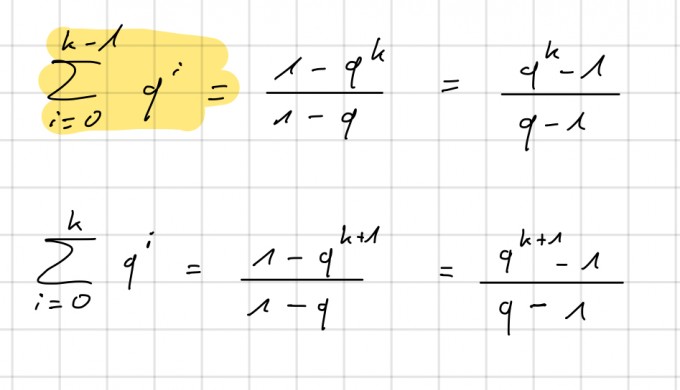
Meine Frage ist, wie die Umformung zusammenhängt. Dies sind ja verschiedene Summen, die nicht durch einen Indexshift zustande gekommen sind. Kann man sich trotzdem erklären, wieso bei der gelb markierten Formel mit der Grenze k-1 in der Umformung der Summe dann nur noch q^k steht?
Außerdem verstehe ich nicht, wieso man bei beiden Formeln im zweiten Gleichungsschritt jeweils die 1 mit dem q^k bzw. dem q^(k+1) tauschen kann.
Ich würde mich sehr über eine Klärung meiner Verwirrung freuen ... Vielen Dank!