Konfidenzintervall oder Normalverteilung berechnen? Symmetrische Intervall rund um den Mittelwert ermitteln

Question

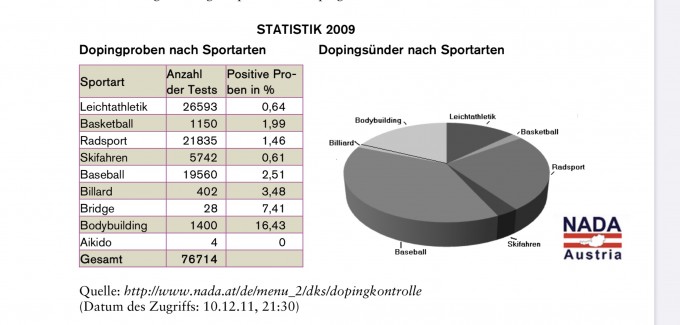
Aufgabe: Doping in Radsport

Ermitteln Sie für die Dopingsünder im Radsport das symmetrische Intervall rund um den Mittelwert, in dem die Wahrscheinlichkeit 95% beträgt und formulieren Sie ihr Ergebnis in Bezug auf die Aufgabenstellung.
Begründen Sie anhand einer geeigneten Skizze, wie diese Aufgabe zu berechnen ist.

Ich weiß nicht, ob man des mit dem Konfidenzintervall rechnen muss oder was anderes?

Ich wäre sehr dankbar, wenn einer mir mit Lösungschritte das erklären könnte?
Problem/Ansatz:

Ich weiß nicht, wie das geht:(

Comments

Ist das eine Rückfrage hierzu? https://www.mathelounge.de/659447/wahrscheinlichkeit-dass-unter-teilnehmern-mehr-gedopt-sind

Answer 1

Gleiche Tabelle wie letzthin. Plötzlich andere Aufgabe? Neue Fragestellung?

Sicher, dass die alten Rechnungen nicht nochmals gemacht werden müssen? Hier mal der Link zu den vorherigen Rechnungen zu dieser Tabelle https://www.mathelounge.de/659447/wahrscheinlichkeit-dass-unter-teilnehmern-mehr-gedopt-sind

Comments

Ich weiß nicht, ob man des mit dem Konfidenzintervall rechnen muss oder was anderes?

Konfidenzintervall könnte eine Antwort sein auf die obige Frage. Studiere mal, was hier getan wurde: https://www.mathelounge.de/41752/in-welchem-symmetrischen-intervall-um-den-mittelwert

Answer 2

μ = n·p = 21835·0.0146 = 318.8
σ = √(n·p·(1 - p)) = √(21835·0.0146·(1 - 0.0146)) = 17.72

Φ(k) = 0.5 + 0.95/2 → k = 1.960

[μ - k·σ ; μ + k·σ] = [318.8 - 1.960·17.72 ; 318.8 + 1.960·17.72] ≈ [284 ; 354]

Unter den 21835 Tests der Radfahrer würde ich also mit einer 95% Wahrscheinlichkeit 284 bis 354 positive Proben erwarten.