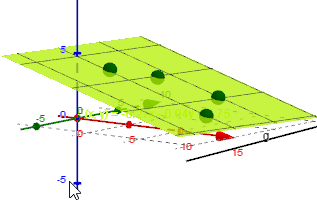
Anpassung an Methode der kleinsten Fehlerquadrate
\(\small f(x, y) \, := \, a_2 \; y + a_1 \; x + a_0\)
\(\small R_k = \left(f\left(X_k, Y_k \right) - Z_k \right)^{2}\)
\(\small R_k(a_2, a_1, a_0) \, := \, \left(a_0 + \frac{25}{2} \; a_1 - \frac{7}{5} \right)^{2} + \left(a_0 + 3 \; a_1 + \frac{1}{5} \; a_2 - 4 \right)^{2} + \left(a_0 + 5 \; a_1 + \frac{7}{2} \; a_2 - \frac{16}{5} \right)^{2} + \left(a_0 + 10 \; a_1 + \frac{23}{5} \; a_2 - 2 \right)^{2}\)
\(\small dR_{a_2,a_1,a_0} \, := \, \left\{ \frac{83}{5} \; a_0 + \frac{641}{5} \; a_1 + \frac{669}{10} \; a_2 - \frac{212}{5}, 61 \; a_0 + \frac{1161}{2} \; a_1 + \frac{641}{5} \; a_2 - 131, 8 \; a_0 + 61 \; a_1 + \frac{83}{5} \; a_2 - \frac{106}{5} \right\} \)
\(F(x, y) \, := \, -0.27 \; x - 0.04 \; y + 4.75\)