Definitionsmenge für f und g bestimmen: f:x → x / (1+5x); g:x → (x+2) / (x2+x-2)

Question

Aufgabe:

a.) Bestimmen Sie die maximale Definitionsmenge der Funktionen f und g. Geben Sie die Art der Definitionslücken an, ob es sich um Polstellen oder um hebbare Definitionslücken handelt.

f:x → x / (1+5x) g:x → (x+2) / (x²+x-2)

b.) Untersuchen Sie, ob bei den Funktionen f und g Asymptoten vorhanden sind und geben Sie gegebenfalls die Geradengleichungen der Asymptoten an.

f:x → (6x²-1) / (3x²+1) g:x → (2x²-1) / (x+1)

c.) Bestimmen Sie die Extrempunkte der Funktionen f und g mit Hilfe des hinreichenden Kriteriums der zweiten Ableitung.

f:x → x² / (x-1) g:x → (2-x³) / 2x

Answer 1

a)

f(x) = x/(1 + 5·x)

D = R \ {-1/5}

Polstelle

g(x) = (x + 2)/(x² + x - 2) = (x + 2)/((x - 1)·(x + 2))

D = R \ {1, -2}

Polstelle bei 1 und Hebbare Definitionslücke bei -2

b.) Untersuchen Sie, ob bei den Funktionen f und g Asymptoten vorhanden sind und geben Sie gegebenfalls die Geradengleichungen der Asymptoten an.

Am einfachsten macht man hier eine Polynomdivision

f(x) = (6·x² - 1)/(3·x² + 1) = 2 - 3/(3·x² + 1) 
Asymptote y = 2

f(x) = (2·x² - 1)/(x + 1) = 2·x - 2 + 1/(x + 1)
Asymptote y = 2x - 2

c.) Bestimmen Sie die Extrempunkte der Funktionen f und g mit Hilfe des hinreichenden Kriteriums der zweiten Ableitung.

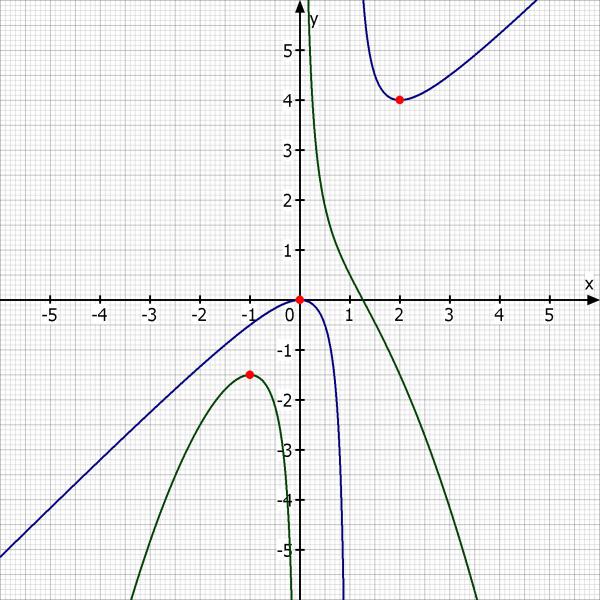
f(x) = x²/(x - 1)
f'(x) = x·(x - 2)/(x - 1)²
f''(x) = 2/(x - 1)³

f'(x) = 0
x·(x - 2) = 0 [Ich brauche bei Brüchen nur den Zähler null setzen]
x = 2 ∨ x = 0

f''(0) = -2
f''(2) = 2

f(0) = 0 [Hochpunkt]
f(2) = 4 [Tiefpunkt]

g(x) = (2 - x³)/(2·x)
g'(x) = - (x³ + 1)/x²
g''(x) = (2 - x³)/x³

g'(x) = 0
(x³ + 1) = 0
x = -1

g''(-1) = -3

g(-1) = -1.5 [Hochpunkt]

Skizze beider Funktionen