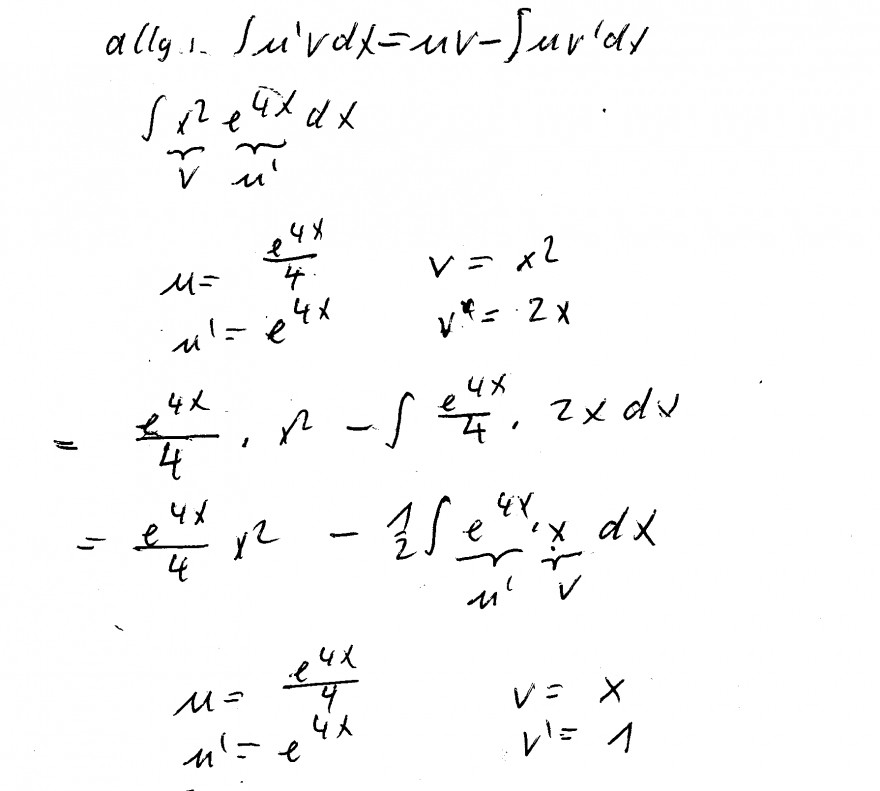Partielle Integration (ist mein Rechenweg richtig?)

Question

$\int x^{2} e^{4 x} d x$

$u=x^{2} \quad v=\frac{1}{4} e^{4 x}$
$u^{\prime}=2 x \quad u^{\prime}=e^{4 x}$

$x^{2} \frac{1}{4} c^{4 x}-2 \cdot \frac{1}{4} \int x e^{4 x}$
$x^{2}-\frac{1}{4} e^{4 x}-\frac{1}{4} x^{2} \frac{1}{4} e^{4 x}+c$
$x^{2}\frac{1}{4} e^{4 x}\left(1-\frac{1}{4}\right)+c$

Answer 1

Hallo,

die 1. partielle Integration ist richtig.

Bei der 2. partiellen Integration hast Du das Integral  ∫ e^(4x) x dx falsch berechnet.

Ich bin auf folgendes Ergebnis gekommen:

=(e^(4x) x²)/4 -( e^(4x) *x)/8 +e^(4x)/32 +C

mann kann noch ein bischen vereinfachen

Es gibt auch Online Integralrechner mit Lösungsweg:

https://www.integralrechner.de/