Wie bestimmt man den Grenzwert dieser Funktionen?

Question

Wie berechnet man

$lim_{x \to 0} ( \frac{1}{x} - \frac{e^x}{sin (x)}$)

und

$lim_{x \to 0} x^{sin(x)}$ ?

L'Hospital hat mich hier nicht so recht weitergebracht, seht ihr andere Möglichkeiten?

Answer 1

Hallo,

zu 1)

Du hast hier den Typ ∞ -∞

Bilde zuerst den Hauptnenner und wende dann L'Hospital an , ggf auch mehrmals

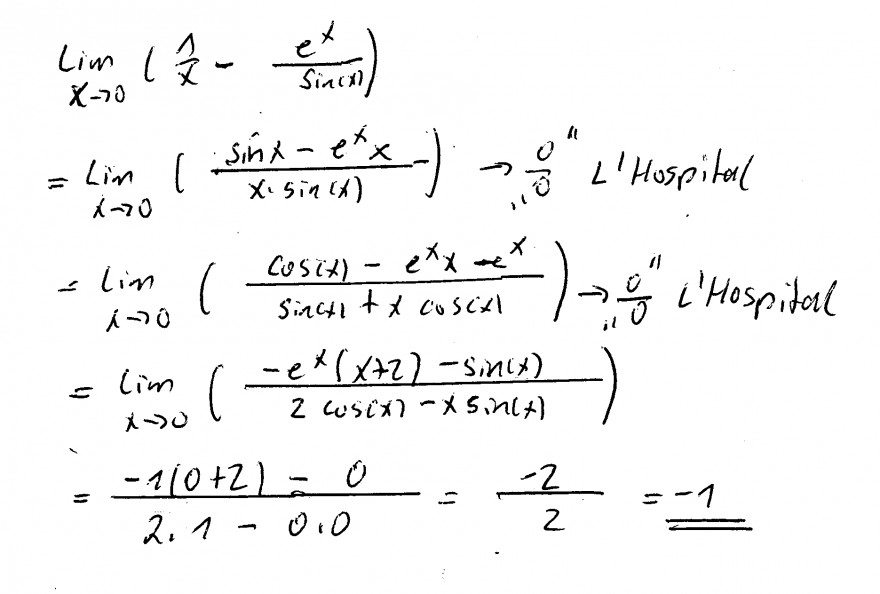
Zu 2)

Du hast hier den Typ 0⁰

gehe hier zur e - Funktion über.

Wende dann L'Hospital an.

$\lim \limits_{x \rightarrow 0} x^{\sin (x)}=1$

Comments

Ahh, verstehe, muchas gracias !!!!

Answer 2

Verwende:

x^(sinx) = e^(sinx*lnx)