Integral Graphen schneiden sich Flächeninhalt berechnen

Question

mal wieder eine Aufgabe bei der ich überfordert bin:

Gegeben sind die beiden Funktionen f und g mit

$$f(x)=\frac{1}{3}x^{3}+2x^{2}+\frac{11}{6}x+2$$ und

$$g(x)=2+\frac{1}{6}x$$

Nun soll den von den Graphen der beiden Funktionen f und g eingeschlossenen Flächeninhalt berechnet werden.

Dazu habe ich erstmals die Schnittpunkte berechnet. Diese sind -5, -1 und 0. Danach muss man etwas mit den Integral machen, aber ich weiß nicht wie.

Answer 1

f = 1/3 * x³ + 2 * x² + 11/6 * x + 2
g = 2 + 1/6 * x

Deine Schnittpunkte sind korrekt

Die Differenzfunktion ist

d = f - g ;

d = x³ / 3 + 2 * x² + 5/3 * x

Stammfunktion
( denn wir wollen ja den Flächeninhalt der
Differenzfunktion ermitteln )

S ( x ) = x⁴ / 12 + 2/3 * x³ + 5 / 6 * x²

Und nun die Integrale zwischen den Schnittpunkten
berechnen
[ S ( x ) ] zwischen -5 und -1
sowie
[ S ( x ) ] zwischen -1 und 0

32/3
- 1/4

Flächen sind immer positiv
abs(32/3)
+
abs(- 1/4)

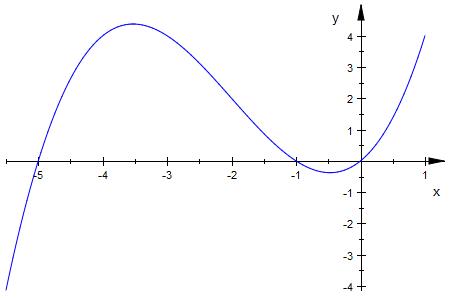
Graph der Differenzfunktion

 Frag nach bis alles klar ist