Hi,
ich gehe gerade einen Lückentext durch und habe einen Satz so ausgefüllt:
4.Ist v ein unitärer Raum mit Orthonoalbasis \( B=(v 1, \ldots, v n), \) und ist
\( x=\sum \limits_{j=1}^{n} y_{j} v_{j} \)
, so gilt \( \left\langle x, v_{1}\right\rangle=0 . \) Mit den Skalarprodukten \( \langle x, vl\rangle \) für IEK \( ^{\text {mxn }} \) berechnet man die Norm von x
also durch
\( I I x I I=\sqrt{<\sum \limits_{j=1}^{n} y_{j} v_{j}, \sum \limits_{j=1}^{n} y_{j} v_{j}>} \)
(Über den zweiten Eintrag sollte eigentlich ein komplex-konjugiert-Strich, ich weiß allerdings nicht wie man das mit Latex macht)
Das ist allerdings die eigentliche Lösung dazu und ich kann die ausgefüllten Lücken jedoch nicht so ganz nachvollziehen:

Text erkannt:
Ist \( v \) ein unitärer Raum mit Orthonoalbasis \( B=(v 1, \ldots, v n), \) und ist
\( \sum \limits_{j=1}^{n} \lambda_{j} v_{j}=x \)
, so gilt \( < X_{1} V_{l}>= \)
\( \sum \limits_{j=1}^{n} \lambda_{j}<v_{j}, v_{l}>=\lambda_{l} \)
Mit den Skalarprodukten
\( <x, v_{l}> \)
für
\( l \in\{1, \dots, n\} \)
berechnet man die Norm von x also durch
\( I I x I I=\sqrt{\sum \limits_{l=1}^{n} I<x, v_{l}>I^{2}} \)
Mein erstes Problem mit der Lösung ist, dass ich nicht verstehe, wo die Betragsstriche geblieben sind. Aber das Hauptproblem von mir ist, dass ich nicht verstehe, was hier gemacht wurde:
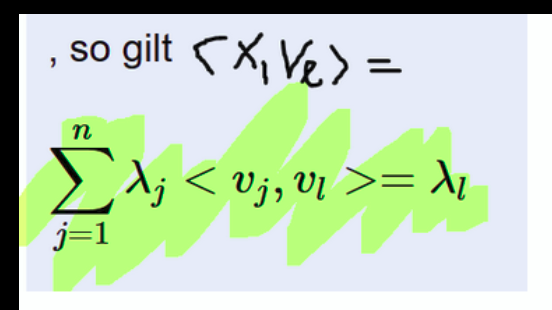
Text erkannt:
so gilt \( \left.\subset x_{1} v_{2}\right\rangle= \)
\( \sum \limits_{j=1}^{n} \lambda_{j}<v_{j}, v_{l}>=\lambda_{l} \)
Wieso darf ich hier vl in die Summe ziehen?
VG:)