Erstmal die Zeichung:
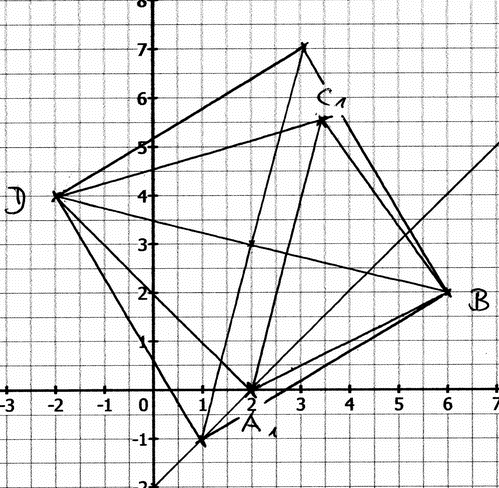
1.0 Die Punkte D ( -2 / 4 ) und B ( 6 / 2 ) legen Drachenvierecke AnBCnD fest mit An ( x / x – 2 ) auf der Geraden g: y = x – 2, G = Q x Q.
1.1 Zeichne den Graph zu g und das Drachenviereck A1BC1D für x = 2 in ein Koordinatensystem.
Platzbedarf: LE 1cm -3 < x < 8 -3 < y < 8
Siehe Zeichnung
1.2 Für welche Werte von x existieren Drachenvierecke AnBCnD? Berechne.
Die Diagonale hat die Steigung -2/8 = -1/4. Die Senkrechte Diagonale muss dann die Steigung 4 haben. Also lege ich zwei lineare Funktionen mit der Steigung 4 durch B und D und berechne den Schnittpunkt mit g.
d1(x) = 4*(x + 2) + 4 = 4x + 12
g(x) = d1(x)
x - 2 = 4x + 12
-3x = 14
x = -14/3
d2(x) = 4*(x - 6) + 2 = 4x - 22
g(x) = d1(x)
x - 2 = 4x - 22
-3x = -20
x = -20/-3 = 20/3
x muss zwischen -14/3 und 20/3 liegen.
1.3 Berechne die Koordinaten von A1 und C1 .
A1(2 | g(2)) = A1(2 | 0)
Ich berechne den Schnittpunkt der Diagonalen indem ich eine Gerade durch A1 lege mit der Steigung 4.
d3(x) = 4*(x - 2) + 0 = 4x - 8
Nun stelle ich noch die Diagonale durch B und D auf
DB(x) = -1/4*(x + 2) + 4 = -1/4 x + 7/2
DB(x) = d3(x)
-1/4 x + 7/2 = 4x - 8
-17/4 x = -23/2
x = 46/17 = 2 + 12/17
Der Punkt C2 Befindet sich dann bei
C2(2 + 12/17 + 12/17 | d3(2 + 12/17 + 12/17))
C2(58/17 | d3(58/17))
C2(58/17 | 96/17)
1.4 Unter den Drachenvierecken gibt es eine Raute A2BC2D. Zeichne sie ein und berechne die Koordinaten von A2 und C2 .
Mittelpunkt zwischen DB befindet sich bei (2 | 3).
d4(x) = 4*(x - 2) + 3 = 4x - 5
Schnittpunkt von g mit d4 g(x) = d4(x)
x - 2 = 4x - 5
-3x = -3
x = 1
A2 befindet sich also bei (1 | 1) und C2 bei (3 | 7)
1.5 Beweise durch Rechnung, dass die Raute A2BC2D ein Quadrat ist.
Wir brauchen nur zeigen das die Diagonalen gleich lang sind. Das sie Senkrecht sind wissen wir ja bereits.
|DB| = Wurzel(2^2 + 8^2) = Wurzel(68)
|A2C2| = Wurzel(2^2 + 8^2) = Wurzel(68)
Damit sind die Diagonalen gleich lang, Halbieren sich gegenseitig und bilden ein 90 Grad winkel. Damit muss die Figur ein Quadrat sein.