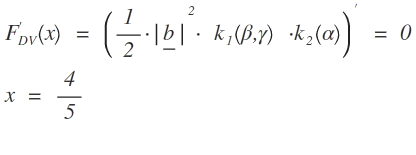Aufgabe zu Drachenvierecken

Question

1.0 Gegeben sind Drachenvierecke ABnCnDn deren Diagonale [ACn] auf der Symmetrieachse liegen. Die Punkte Bn (x | y) liegen auf der Geraden g mit y=0.5x - 2. Die Winkel BnADn haben stets das Maß 73,74° und die Winkel CnBnA das Maß 123,69°. Es gilt A (0|0)

 

1.1 Zeichne die Drachenvierecke AB1C1D1 und AB2C2D2 für x=4 und x=6

1.2 Stelle die Koordinaten der Punkte Dn in Abhängigkeit der Abszisse x der Punkte Bn dar.

1.3 Die Punkte Bn lassen sich auf die Punkte Cn abbilden. Stelle die Koordinaten der Punkte Cn in Abhängigkeit von der Abszisse x der Punkte Bn dar.

1.4 Berechne die Belegung von x, für die die Diagonale [B3D3] auf der Geraden g verläuft.

1.5 Berechne die Belegung von x, für die das Drachenviereck AB4C4D4 einen Flächeninhalt von 37,9 FE hat.

1.6 Berechne die Belegung von x, für die das Drachenviereck AB0C0D0 minimalen Flächininhalt hat.

1.7 Berechne die Belegung von x (x>2,5) für die die Strecke [B5C5] mit der Geraden g einen Winkel mit dem Maß 20° bildet.

Answer 1

Aufgabe Drachenvierecke

Angaben:
* Diagonale [ACn] liegt auf Symmetrieachse
* Bn (x | y) ∈ g: y(x) =0.5x - 2
* ∠ BnADn = 73,74°
* ∠ CnBnA = 123,69°
* A (0|0)

Ergänzungen:
* ∠ BnADn = α = 73,74°
* ∠ CnBnA  = β = 123,69°
* ∠ BnCnDn = γ = 38,88°
* ∠ CnDnA = α = 73,74°  //Drachenviereck

 

1.1 Zeichne die Drachenvierecke AB1C1D1 und AB2C2D2 für x=4 und x=6
Hier eine Zeichnung für x = 2.

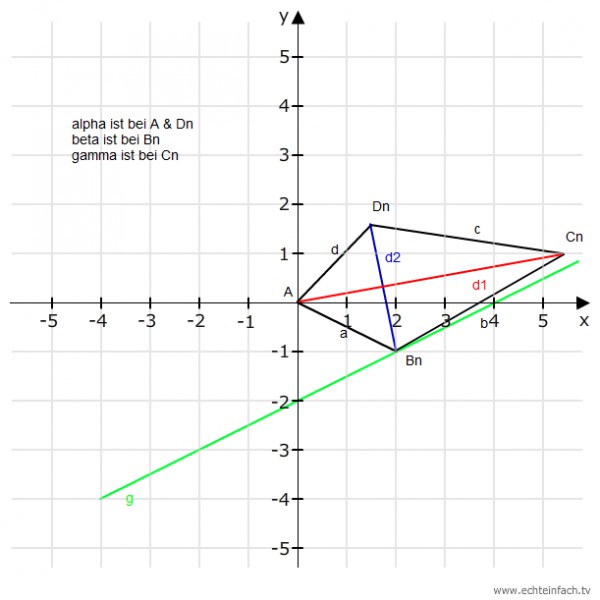
1.2 Stelle die Koordinaten der Punkte Dn in Abhängigkeit der Abszisse x der Punkte Bn dar
Vektor auf Punkt Bn(x | 0.5x - 2) und Betrag des Vektors:


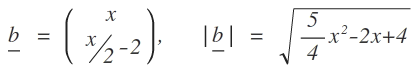
Der Vektor d auf Dn ergibt sich aus der Drehung des Vektors b um den Ursprung mit dem Winkel α:

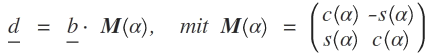
M heißt Drehmatrix;s( ) = sin( ), c( ) = cos( ).

 

1.3 Stelle die Koordinaten der Punkte Cn in Abhängigkeit von der Abszisse x der Punkte Bn dar
Der Vektor c auf Cn ergibt sich aus der Drehung von b um den Ursprung mit α/2, Normierung und Streckung mit d₁ der Länge der Diagonalen, die auf der Symmetrieachse liegt.

Berechnung der Länge von d₁ mit dem Sinussatz:

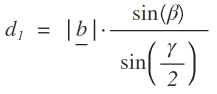
Formel für Vektor c:

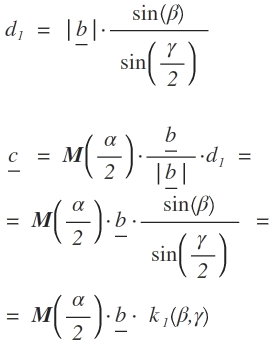
k₁(β,γ) ist eine Konstante die in Abhängigkeit von β und γ berechnet wird; sie dient nur der Übersichtlichkeit.

1.4 Berechne die Belegung von x, für die die Diagonale [B3D3] auf der Geraden g verläuft
Wenn dies der Fall sein soll muss D₃ ∈ g gelten, x muss die Geradengleichung erfüllen. Man setzt die x- und y-Werte des Vektors d in die Geradengleichung ein und löst nach x auf.

 

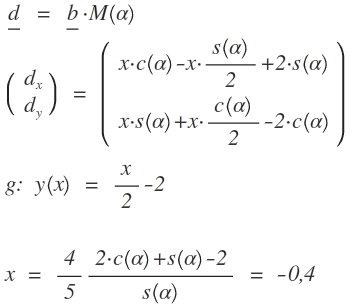
1.5 Berechne die Belegung von x, für die das Drachenviereck AB4C4D4 einen Flächeninhalt von 37,9 FE hat
Der Flächeninhalt eines Drachenvierecks berechnet sich aus F_DV= 1/2 *d₁*d₂.

Die Länge der Diagonalen d₂ berechnet sich mit Hilfe des Sinussatzes zu:

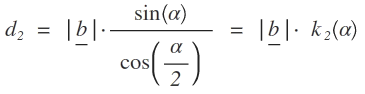
Nach F_DV= 1/2 *d₁*d₂:

 

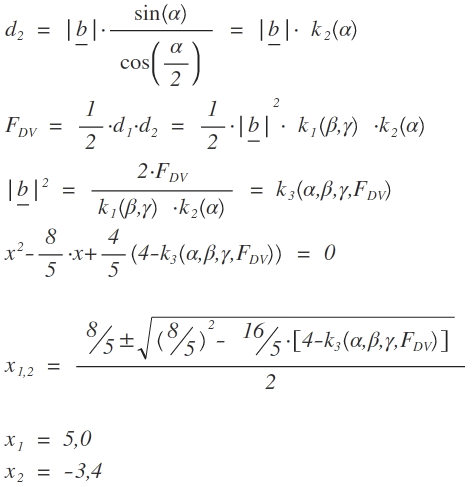
1.6 Berechne die Belegung von x, für die das Drachenviereck AB0C0D0 minimalen Flächininhalt hat
Die Fläche wird minimal, wenn die Ableitung 0 ist. F'_DV(x) = 0

Comments

Wär schön, wenn jemand das bestätigen könnte.

(1.7 fehlt noch)

---

klasse Antworten

---

Naja, aber kann man damit auch was anfangen? Ich hab es jetzt mal so gelöst, wie es mir am einfachsten erschien. Ich kenn den Hintergrund des Fragenstellers nicht. Kann sein, dass er mit Matrizen noch nichts anfangen kann.

---

Vorsicht!

Bei 1.2 und 1.4 muss es M *b heißen, sonst funktioniert die Rechnung nicht.