Hallo,
Die orthogonale Abbildung \(\varphi\) ist eine Rotation. Jetzt muss man noch wissen, dass eine Drehung auch als zweifache (Achsen-)Spiegelung dargestellt werden kann, und der Winkel zwischen den Spiegelachsen gleich dem halben Drehwinkel ist. Ich berechne nun nicht den Drehwinkel \(\alpha\), sondern nur seinen Tangens, indem ich den Einheitsvektor in X-Richtung mit \(\varphi\) abbilde$$\varphi(e_x) = \begin{pmatrix} 3 \\ 4\end{pmatrix} \implies \tan \alpha = \frac 43$$nach der Halbwinkelformel ist $$\tan \frac{\alpha}2 = \frac{1 - \cos \alpha}{\sin \alpha} = \frac{1 - \frac 35}{ \frac 45} = \frac 12$$Da man die Lage der Spiegelachsen frei wählen kann, mehme ich als erste die X-Achse und als zweite Achse dann eine Gerade, die mit der X-Achse den Wert \(\alpha/2\) einschließt. Nach \(\tan(\alpha/2) = 1/2\) ist das die Gerade, die z.B. durch den Punkt \((2;1)\) verläuft.
Folgende Skizze zeigt das:
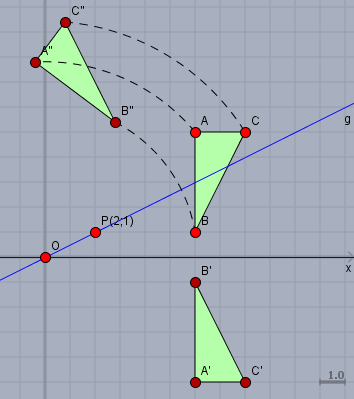
Der analytische Weg geht so:
Die Matrix \(S\) einer Spiegelung kann wie folgt dargestellt werden:$$S = \underline 1 - 2n\cdot n^T, \quad |n| = 1$$wobei \(n\) der Vektor ist, der senkrecht auf der Spiegelachse steht. Wähle ich als erste Achse wieder die X-Achse, so ist $$n= \begin{pmatrix}0\\ 1\end{pmatrix} \implies S(n) = \begin{pmatrix}1& 0\\ 0& -1\end{pmatrix}$$Nun muss es noch eine zweite Spiegelachse - definiert durch \(u\) - geben, für die folgendes gilt$$(\underline 1 - 2u\cdot u^T) \cdot S(n) = \frac 15 \begin{pmatrix} 3& -4\\ 4& 3 \end{pmatrix}$$Auflösen nach \(S(u)\) bzw. \(u\) gibt dann$$S(u) = \frac 15 \begin{pmatrix}3& 4\\ 4& -3\end{pmatrix}, \quad u = \frac 1{\sqrt 5} \begin{pmatrix}1\\ -2\end{pmatrix}$$