Ableitung einer Funktion (produktregel, quotientenregel)

Question

Bei dieser Ableitung kommt bei mir etwas völlig anderes raus obwohl ich meine, alles richtig gerechnet zu haben. Das wäre mein Ergebnis: (ich habe zuerst die Produkt- und dann die Quotientenregel angewendet.)

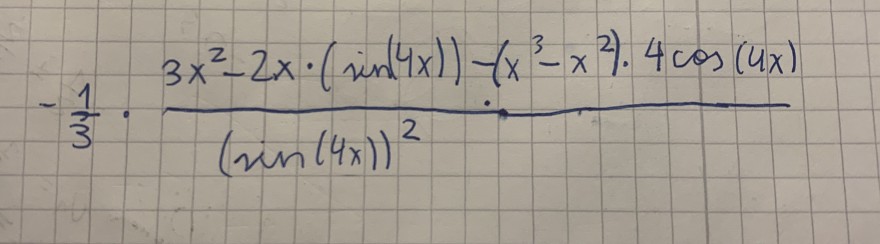
Text erkannt:

$-\frac{1}{3} \cdot \frac{3 x^{2}-2 x \cdot(\sin (4 x))-\left(x^{3}-x^{2}\right) \cdot 4 \cos (4 x)}{(\sin (4 x))^{2}}$

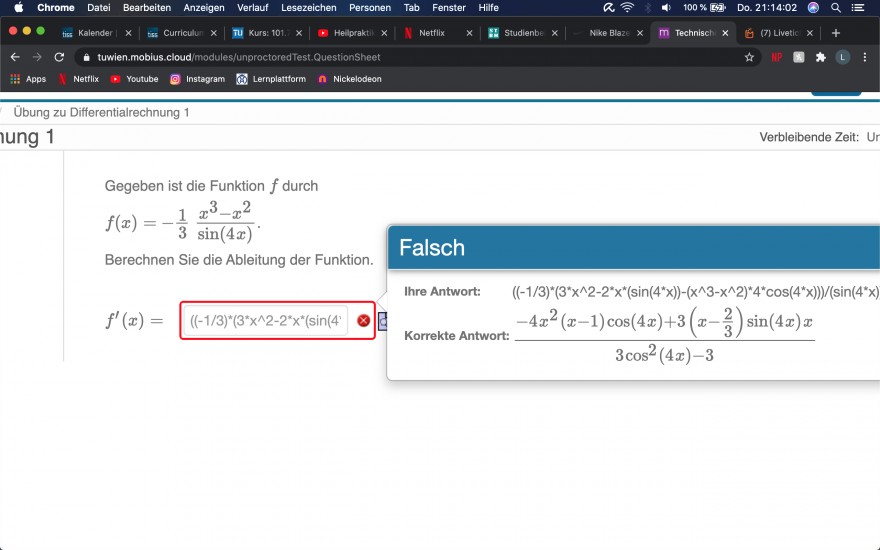
Das hier steht aber in der Lösung:

Text erkannt:

年
華 Apps
Öbung zu Differentialrechnung 1
vung 1 Ve
Gegeben ist die Funktion $f$ durch $f(x)=-\frac{1}{3} \frac{x^{3}-x^{2}}{\sin (4 x)}$

Comments

wie man auf das unter dem Bruch kommt, ist für mich absolut unverständlich.

Answer 1

Aloha :)

Dein Ergebnis ist (fast) richtig, du hast nur die Klammer um den ersten Term im Zähler vergessen:$$f'(x)=\left(-\frac{1}{3}\cdot\frac{\overbrace{x^3-x^2}^{=u}}{\underbrace{\sin(4x)}_{=v}}\right)'$$$$\phantom{f'(x)}=-\frac{1}{3}\cdot\frac{\overbrace{(3x^2-2x)}^{=u'}\cdot\overbrace{\sin(4x)}^{=v}-\overbrace{(x^3-x^2)}^{=u}\cdot\overbrace{\underbrace{\cos(4x)}_{=\text{äußere}}\cdot\underbrace{4}_{=\text{innere}}}^{=v'}}{\sin^2(4x)}$$$$\phantom{f'(x)}=-\frac{1}{3}\cdot\frac{(3x^2-2x)\cdot\sin(4x)-4(x^3-x^2)\cos(4x)}{\sin^2(4x)}$$$$\phantom{f'(x)}=\frac{4x^2(x-1)\cos(4x)-x(3x-2)\sin(4x)}{3\sin^2(4x)}$$Das ist dasselbe Ergebnis wie in der Musterlösung. Dort wurde nur der Nenner maximal kompliziert hingeschrieben:$$3\cos^2(4x)-3=3[\cos^2(4x)-1)]=3[\cos^2(4x)-(\sin^2(4x)+\cos^2(4x))]$$$$=3[-\sin^2(4x)]=-3\sin^2(4x)$$