Matrixnorm und Maximumsnorm

Question

Aufgabe:

Text erkannt:

(c) Geben Sie die $\|\cdot\|_{T}$ zugeordnete Matrixnorm
$$\|A\|_{T}:=\sup _{x \neq 0} \frac{\|A x\|_{T}}{\|x\|_{T}}$$
explizit durch die Matrixnorm $\|.\|_{\infty}$ an.

Problem/Ansatz:

Ich weiß gar nicht wie ich an diese Aufgabe rangehen soll. T ist angegeben als T=(-3, 1; 1, 2) und außerdem gilt: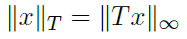

Text erkannt:

$\|x\|_{T}=\|T x\|_{\infty}$

Wenn ich die T-Norm einfach in die Maximumsnorm umschreiben, dann habe ich ja auch nichts gewonnen. Weiß hier einer weiter?

Answer 1

Wenn man $\| A \|_\infty$ ausschreibt, s. https://de.wikipedia.org/wiki/Zeilensummennorm, kommt man auf $$\| A \|_\infty = \text{max}_{ i=1 \cdots n } \sum_{j=1}^n \left| a_{ij} \right|$$ Bei Deiner Matrix $$A = \begin{pmatrix} -3 & 1 \\ 1 & 2 \end{pmatrix}$$

ergibt sich also $$\| A \|_\infty = \text {max} \{ 4,3 \} = 4$$