Berechnen sie alle werte für c so, dass die vom Graphen von f und den Koordinatenachsen vollständig begrenzte Fläche …

Question

Aufgabe:

Eine funktion g ist durch g(x)=e^(-x)-x^2+c.

Berechnen sie alle werte für c so, dass die vom Graphen von f und den Koordinatenachsen vollständig begrenzte Fläche den Inhalt 2 FE besitzt

Problem/Ansatz:

Ich weiß echt nicht wie ich das berechnen soll . Bitte heöfen sie mir

Comments

Was ist f? Meinst du vielleicht \(f(x)=e^{-x}-x^2+c\)?

---

f(x)= e^-x - x^2

g(x) = f(x) +c

---

g(x)=e^-x-x^2+c

Integrationsgrenzen:

x_1=0

e^-x-x^2+c=0 nach x auflösen.

x_2=...

mfG

Moliets

---

Wie berechne ich nun die richtigen Werte für c ?

mfG

Moliets

---

Mir ist nichts Neues dazu eingefallen.
@Fragesteller
Ist sonst noch etwas angegeben ?
Stell mal die Frage als Foto der Buchseite ein.

---

Gast hj2166 hat doch so schön geantwortet. Wie können wir ihn erreichen?

mfG

Moliets

---

Hallo Peter,

da du hier inzwischen munter weitere Fragen eingibst: Hast du das hier:

https://www.mathelounge.de/763739/berechnen-sie-den-wert-c

inzwischen lösen können oder hast du aufgegeben?

Answer 1

Den Lösungsweg häppchenweise

1.Zeile : die Funktion
2. Nullstelle
e^(-x) - x^2 + c = 0
c = e^(-x) - x^2 ( hier n genannt )
3. Stammfunktion von f
4.s ( 0 )
5. s bei der Nullstelle n
( obere Integrationsgrenze )
Integrationsfunktion ( oben minus unten )

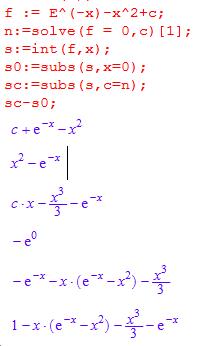
als nächster Schritt wird folgen
Fläche = 2( sc - sn ) = 2
beziehungsweise
Fläche - 2 = 0
Ein Fall für das Newtonsche Näherungsverfahren

Es gibt 2 Lösungen
x = 1.342 und umgerechnet c = x^2 - e^(-x)
c = 1.54

x = -1.811 => c = -2.8368

Die Wertepaare in f eingesetzt ergeben
A = 2

mfg

Comments

Text erkannt:

Welche \( x \) erfüllen die Menge \( R \)
\( |x|-1=\frac{1}{2} x \)
\( |x|=\frac{1}{2} x+1 \)
\( \sqrt{x^{2}}=\frac{1}{2} x+\left.1\right|^{2} \)
\( x^{2}=\frac{1}{4} x^{2}+x+1 \)
\( \frac{3}{4} x^{2}-x=1 \mid \cdot \frac{4}{3} \)
\( x^{2}-\frac{4}{3} x=\frac{4}{3} \mid+q \cdot E \cdot\left(\frac{-\frac{4}{3}}{2}\right)^{2}=\frac{4}{9} \)
\( x^{2}-\frac{4}{3} x+\frac{4}{9}=\frac{4}{3}+\frac{4}{9}=\frac{16}{9} \)
\( \left(x-\frac{2}{3}\right)^{2}=\frac{16}{9} \)
\( x_{1}=\frac{2}{3}+\frac{4}{3}=2 \)
\( x_{2}=\frac{2}{3}-\frac{4}{3}=-\frac{2}{3} \)
\( \mathrm{mfG} \)
Moliets

Text erkannt:

[) \( g(x)=-x-10 \)
\begin{tabular}{l}
-1. \\
\hline
\end{tabular}
Täche von DAE = 5

---

Leider verstehe ich deine Rechnung überhaupt nicht.
Meine Rechnung stimmt.
Sage mir bitte in welcher Zeile du etwas
nicht verstehst.

---

Entschuldigung: Die Berechnung stimmt zu meiner Zeichnung nicht. Da habe ich die falsche Datei geschickt. Diese schicke ich dir, wenn ich sie wieder fertig habe.

Mein Problem liegt darin, dass ich die nötige Nullstelle in Abhängigkeit zu c nicht finde.

mfG

Moliets

---

Ich suche c in Abhängigkeit von x
f (x ) = e^(-x) - x^2 + c
Nullstelle
f ( x ) = e^(-x) - x^2 + c = 0
c = - e^(-x) + x^2

In Worten :
das c der Nullstelle entspricht ...
dem x der Nullstelle mit angegeben Term
c und x sind die Werte die gesucht sind
damit A = 2

---

Ich meinte  c = - e^(-x) + x^2 nach x aufgelöst.

mfG

Moliets

---

Brauchst du nicht.
Ist wahrscheinlich auch zu kompliziert
oder gar nicht möglich.

---

Stammfunktion von f bilden und schon
einmal 0 als untere Grenze einsetzen.

Ich schaue jetzt aber erst einmal fern.

---

Text erkannt:

Hier die richtige Datei:
\( f(x)=-x+1 \)
\( g(x)=-x+1+c \)
1. Nullstelle ist \( x=0 \)
2. Nullstelle:
\( -x+1+c=0 \)
\( x=c+1 \)
\( 5=\int \limits_{0}^{c+1}(-x+1+c) \cdot d x=\left[-\frac{x^{2}}{2}+x+c \cdot x\right]_{0}^{c+1}=\left[-\frac{(c+1)^{2}}{2}+(c+1)+c \cdot(c+1)\right] \)
\( 10=\left[-(c+1)^{2}+2 \cdot(c+1)+2 \cdot c \cdot(c+1)\right] \)
\( c_{1}=\sqrt{10}-1 \)
\( c_{2}=-\sqrt{10}-1 \)
1.) \( g(x)=-x+1+\sqrt{10}-1=-x+\sqrt{10} \)
2.) \( g(x)=-x+1-\sqrt{10}-1=-x-\sqrt{10} \)
Bei dieser Aufgabe bekommt man ja sofort die beiden "c".
Bei \( g(x)=e^{-x}-x^{2}+c \) hat mir das ja "Bauchweh" bereitet: Wie finde ich die \( 2 . \) Nullstelle?
Bei obiger Aufgabe kommt man ja auf Anhieb zur Lösung.
\( \mathrm{mfG} \)
Moliets

---

Die Aufgabe hat mich an den Rand des Wahnsinns getrieben sondern auch ein bißchen
drüber hinaus.
ich bin mir jetzt aber sicher und muß dir das
nur noch verständlich kommunizieren.

f ( x ) = e^(-x) - x^2 + c
Stammfunktion
S ( x ) = [ c * x ]  - [ x^3 / 3 ] - e^(-x)
Für die untere Grenze gilt x = 0
S ( 0 ) = - e^0 = -1
Bei der oberen Grenze stört das in der
Stammfunktion 2 Variable sind . c und x
Nullstelle : f ( x ) = e^(-x) - x^2 + c = 0
Ich nenne die x Stelle der Nullstelle
xn.
e^(-xn) - xn^2 + c = 0
c = xn^2 - e^(-xn)
Jetzt tausche ich in der Stammfunktion
c durch xn^2 - e^(-xn) aus
S ( x ) = [ (xn^2 - e^(-xn) ) * x ]  - [ x^3 / 3 ] - e^(-x)
Jetzt setze ich als obere Grenze für x = xn ein
S ( oben ) = [ (xn^2 - e^(-xn) ) * xn ]  - [ (xn)^3 / 3 ] - e^(-xn)
s ( oben ) minus s ( unten ) = 2
Und weils so schön ist schreibe ich wieder
für xn = x
[ (x^2 - e^(-x) ) * x ]  - [ (x)^3 / 3 ] - e^(-x) -( -1 ) = 2

oder
[ (x^2 - e^(-x) ) * x ]  - [ (x)^3 / 3 ] - e^(-x) + 1 -2 = 0
[ (x^2 - e^(-x) ) * x ]  - [ (x)^3 / 3 ] - e^(-x) + 1 -2 = 0
[ (x^2 - e^(-x) ) * x ]  - [ (x)^3 / 3 ] - e^(-x) - 1 
= 0
Jetzt das Newtonsche Näherungverfahren
verwenden ergibt die in meiner Antwort
angeführten Wertepaare.

Ich weiß nicht ob ich mit meinem Lösungsweg
mit x und xn nicht irgendwie doppelt
gemoppelt habe. Es stimmt aber.

---

Danke dir! Muss mich nun erst noch darin vertiefen.

mfG

Moliets

Answer 2

Alternative Lösung :

 

Answer 3

Text erkannt:

Eine Funktion \( g \) ist durch \( g(x)=e^{-x}-x^{2}+c \)
Berechnen sie alle werte für \( c \) so, dass die vom Graphen von \( f \) und den Koordinatenachsen vollständig begrenzte
Fläche den Inhalt \( 2 \mathrm{FE} \) besitzt
\( 2=\int \limits_{0}^{c}\left(e^{-x}-x^{2}+c\right) \cdot d x=\left[-\frac{1}{e^{x}}-\frac{x^{3}}{3}+c \cdot x\right]_{0}^{c}=\left[-\frac{1}{e^{c}}-\frac{c^{3}}{3}+c \cdot c\right]-\left[-\frac{1}{e^{0}}-\frac{0^{3}}{3}+c \cdot 0\right] \)
\( 1=\left[-\frac{1}{e^{c}}-\frac{c^{3}}{3}+c^{2}\right]= \)
Mit Wolfram:
\( c_{1} \approx 1,608 \)
\( c_{2} \approx 2,46 \)
\( \mathrm{mfG} \)
Moliets

Comments

Hallo moliets,
wie kommst du auf " c " als integrationsgrenze ?
Es müßte doch der Nullpunkt genommen
werden.
mfg Georg

---

Hallo Georg, ich war irrtümlich der Meinung, dass c die Integrationgrenze ist.

Bloß wie komme ich nun an die Werte , wie Gast hj2166 sie im Bild hat?

mfG

Moliets

---

Meine Rechnung ist ja nun nicht mehr als beste Antwort zu bezeichnen, weil sie schlichtweg falsch ist.

mfG

Moliets

---

Hallo moliets,

nach zähem Ringen habe ich
c = 1.54
f(x) = e^(-x) - x^2 + 1.54
Integral zwischen 0 und 1.342 = 2
heraus.
Ich muß den Rechenweg aber erst einmal
sortieren.
mfg Georg