Wie hoch ist denn der Einsatz von Faktor L im Kostenminimum?

Question

Ein Unternehmen weist folgende Produktionsfunktion F(K,L) mit den Inputfaktoren K für Kapital und L für Arbeit auf

F(K,L)=K+L0.5
Der Preis für eine Einheit Kapital beträgt pK=12 und der Preis für eine Einheit Arbeit beträgt pL=0.55. Minimieren Sie die Kosten des Unternehmens unter Berücksichtigung seiner Produktionsfunktion, wenn ein Output von 210 ME produziert werden soll.

a. Wie hoch ist der Einsatz von Faktor L im Kostenminimum?
b. Wie hoch ist der Einsatz von Faktor K im Kostenminimum?
c. Welchen Wert hat der Lagrange-Multiplikator λ im Kostenminimum?
d. Wie hoch sind in diesem Fall die minimalen Kosten?

ich bekomme heraus

a) 199.01

b) 199.08

c) 2454.42

d) 12.00

Answer 1

Hallo

a)+0,5b) sollten doch wohl 210 geben?

und die minimalen Kosten sollten wirklich weniger als 1 K und 1 L sein?

Schreib bitte nicht nur Ergebnisse, sondern wenigstens deine Ansätze , wir können kontrollieren aber warum sollen wir das alles neu rechnen?

lul

Comments

ich habe so gerechnet:

L=12K+0,55L-λ•K-λ•L^0,5

L’K=12-λ

L’F=0,55-0,5L^-0,5 •λ

λ=12

L’F=0 und λ einsetzen

L=119,01

F=K+L^0,5

210=K+119,01^0,5

K= 199,08

C=12*199,08+0,55*119,01

=2454,42

---

kann das jetzt so stimmen?

Answer 2

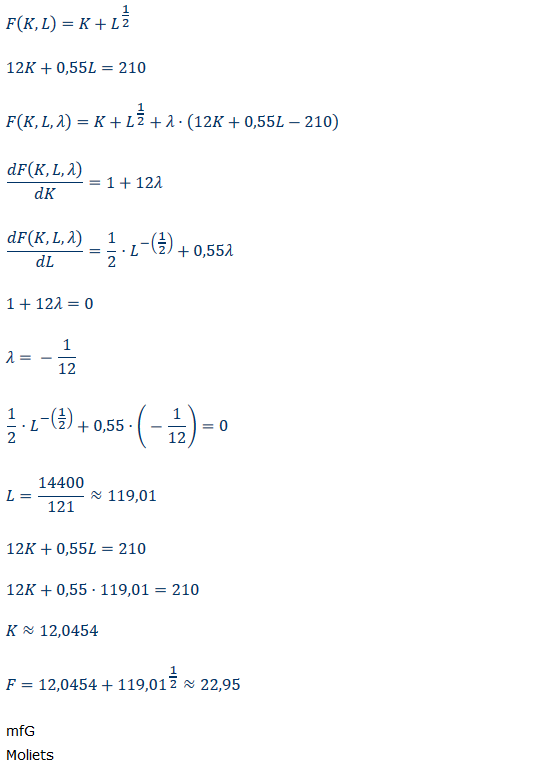
Text erkannt:

$F(K, L)=K+L^{\frac{1}{2}}$
$12 K+0,55 L=210$
$F(K, L, \lambda)=K+L^{\frac{1}{2}}+\lambda \cdot(12 K+0,55 L-210)$
$\frac{d F(K, L, \lambda)}{d K}=1+12 \lambda$
$\frac{d F(K, L, \lambda)}{d L}=\frac{1}{2} \cdot L^{-\left(\frac{1}{2}\right)}+0,55 \lambda$
$1+12 \lambda=0$
$\lambda=-\frac{1}{12}$
$\frac{1}{2} \cdot L^{-\left(\frac{1}{2}\right)}+0,55 \cdot\left(-\frac{1}{12}\right)=0$
$L=\frac{14400}{121} \approx 119,01$
$12 K+0,55 L=210$
$12 K+0,55 \cdot 119,01=210$
$K \approx 12,0454$
$F=12,0454+119,01^{\frac{1}{2}} \approx 22,95$
$\mathrm{mfG}$