p(2l4) , q(4l2) und r(6l4) gehen. Additionsverfahren mit 2 Variablen verstehe ich, mit drei leider nicht... Also erstmal muss ich alles einsetzten in ax Quadrat +bx +c,
1. 4 = 4a + 2b + c
2. 2 = 16a + 4b + c
3. 4 = 36a + 6 b + c
------------------------------------ Erst mal daraus 2 Gleichungen mit 2 Unbekannten machen; c eliminieren
3.-1. 0 = 32a + 4b
2.-1. -2 = 12a + 2b |*2
-------------------------------------
4. 0 = 32a + 4b
5. -4 = 24a + 4b
------------------------------------
4.-5. 4 = 8a |: 8
a=0.5
In 4. einsetzen
0 = 16 + 4b ---------> b= -4
In 1. 4 = 4a + 2b + c einsetzen
4 = 2 - 8 + c -----------> c=10
y= 0.5x2 - 4x + 10
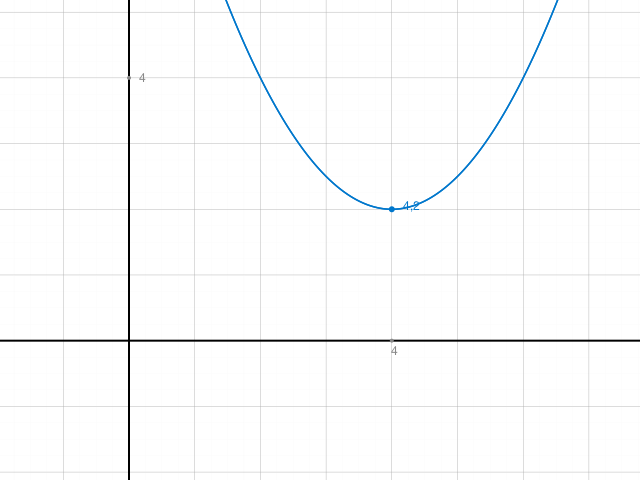
Kontrolle: Plot zeichnen und Punkte überprüfen: -- ok.