Ableitung der Umkehrfunktion. f(x) = ln(2x+1)

Question

Hallo zusammen,

folgende Funktion wird betrachtet:



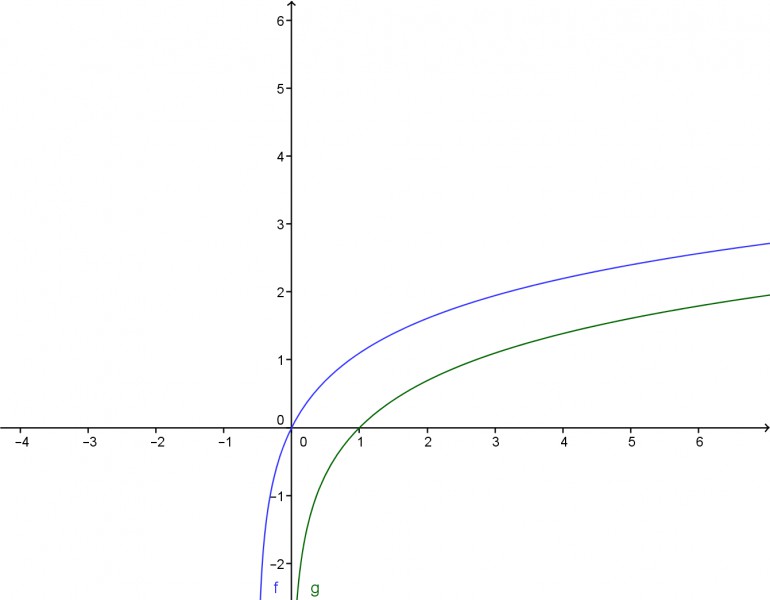
a) Schrittweise Skizzierung der Funktion f(x), indem mit der zugrundeliegenden Funktion g(x)= ln(x) begonnen wird und dann die entsprechenden Transformationen nachvollzogen werden.

b) Welchen Definitions- und welchen Wertebereich hat f(x) ?

c) Für welche x ist f umkehrbar? Berechnung der Umkehrfunktion f^-1 von f.

d) Skizzierung der Graphen von f(x) und  f^-1(x).

e) Berechnung der Ableitung zuerst von f^-1(x) und dann damit die Ableitung von f(x).

f) Skizzierung der Graphen der Ableitungen df(x)/dx und df^-1(x)/dx.


Unten habe ich Lösungsansätze verfasst. Wenn etwas nicht korrekt sein sollte, bitte ich um Korrektur.

,



Lösungsansätze:

Comments

Hallo Robbie2210,

  zum Def Bereich :

  ln(2x+1)
  2x + 1 > 0
  2x > -1
  x > -1/2

  siehe deine eigene Skizze

  mfg Georg

Answer 1

DB von f(x):

ln(2x+1) existiert, wenn 2x+1 > 0
d.h.

2x > -1

x> -0.5

DB= { x Element R | x> -0.5}
Da f streng monoton steigend:

WB der Umkehrfunktion auch  { x Element R | x> -0.5}
Rest und Graphen sehen ok. aus.

f^{-'} sieht unklar aus. Gib dieser Umkehrfunktion einen Namen. Bsp. f^{-1} (x) = g(x) = (e^x -1)/2

Dann g'(x) = e^x / 2
Versuche vielleicht zur Kontrolle noch die Funktion und die Umkehrfunktion zusammen mit y=x, y = -0.5 und x= -0.5 alles ins gleiche Koordinatensystem zu zeichnen. Z.B. damit https://www.matheretter.de/tools/funktionsplotter/

Comments

Hallo Lu,

vielen Dank für deine schnelle Antwort. Ich werde nochmals die Funktion sowie die Umkehrfunktion im Koordinatensystem einzeichnen. Für deine Bemühung habe ich dir 1 Stern sowie 1 Punkt vergeben.

Ich wünsche dir noch einen schönen Abend



PS: Ebenfalls Dankeschön an georgborn, der mir ebenfalls unterstützt hat.