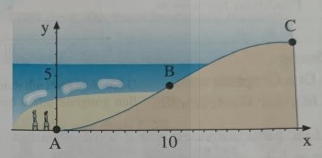
Aufgabe Strandpromenade:
Der Aufgang der Strandpromenade zu einem \( 8 \mathrm{~m} \) hohen Deich soll in der Waagerechten \( 20 \mathrm{~m} \) lang sein. Das Planungsbüro erwägt mehrere Varianten.
a) Variante 1: Die Trassenführung wird durch eine trigonometrische Funktion durch die Punkte A und C realisiert. Dabei soll die Funktion in den Anschlusspunkten A und C die Steigung null haben. Geben Sie die Funktionsgleichung für diese Variante an. Zur Kontrolle: \( \mathrm{f}(\mathrm{x})=4 \cdot \sin \left(\frac{\pi}{20}(\mathrm{x}-10)\right)+4 \)
b) Variante 2: Die Trassenführung wird durch eine ganzrationale Funktion realisiert, die in den Anschlusspunkten \( \mathrm{A} \) und \( \mathrm{C} \) die Steigung null hat. Bestimmen Sie die Funktionsgleichung.
c) Berechnen Sie für beide Lösungen den stärksten Anstieg.
d) Der Aufgang soll \( 2 \mathrm{~m} \) breit sein. Bei welcher Trasse wird weniger Sand als Untergrund benötigt?
e) Variante 3: Diese Variante sieht vor, die Punkte \( A \) und \( B \) durch eine Funktion \( h_{1}(x)=e^{a x}-b \) und die Punkte \( \mathrm{B} \) und \( \mathrm{C} \) durch eine Funktion \( \mathrm{h}_{2}(\mathrm{x})=10-\mathrm{ce}^{-\mathrm{dx}} \mathrm{zu} \) verbinden. Stellen Sie die Funktionsgleichungen auf.
f) Variante 3 soll nur dann vorgeschlagen werden, wenn in den Übergangspunkten \( \mathrm{A}, \mathrm{B} \) und C der Winkel zwischen den beiden Trassenteilen bzw. zwischen jeweils einem Trassenteil und der unteren bzw. oberen Ebene kleiner als \( 10^{\circ} \) ist. Prüfen Sie, ob diese Bedingung erfüllt ist.