Wie beweise ich den Kosinussatz?

Question

Aufgabe:

Beweisen Sie den Kosinussatz

$$ c^{2}=a^{2}+b^{2}-2 a b \cdot \cos (\gamma) $$

wobei die übliche Bezeichnung für Dreiecke gilt. Interpretieren Sie die Längen einer Strecke als Betrag eines Vektors \( (a=|\vec{a}|) \) und verwenden Sie \( \vec{b}+\vec{c}=\vec{a} \).

Answer 1

Hallo,

Ich mache mal eine Skizze:

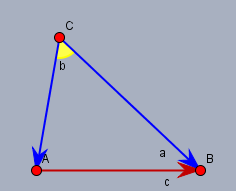
der Winkel \(\gamma\) (gelb) wird von den Vektoren \(\vec b\) und \(\vec a\) (blau) eingeschlossen. Das Skalarprodukt der Vektoren \(\vec b\) und \(\vec a\) (mit dem Winkel \(\gamma\)) ist:$$\vec a \cdot \vec b = |\vec a| \cdot |\vec b| \cdot \cos \gamma, \quad |\vec a| =a,\space |\vec b| = b$$wenn man nun die Vektorsumme nach \(\vec c\) auflöst und quadriert$$\begin{aligned}\vec c &= \vec a - \vec b &&\left|\,{}^2 \right. \\ \vec c^2 &=  (\vec a - \vec b)^2 \\ &= \vec a^2 - 2\vec a \vec b + \vec b^2 \end{aligned}$$Jetzt berücksichtige ich noch, dass für jeden Vektor \(\vec v\) gilt: $$\vec v^2 = |\vec v|^2 = v^2$$zusammen mit dem Skalarprodukt von oben erhält man dann:$$\begin{aligned} \vec c^2 &= \vec a^2 - 2\vec a \vec b + \vec b^2 \\ c^2 &= a^2 + b^2 - 2ab\cos \gamma\end{aligned}$$