Berechnen sie On und Un für die Funktion f über dem Intervall |.

Question

Aufgabe:

Berechnen sie O_n und Un für die Funktion f über dem Intervall |. Welcher Grenzwert ergibt sich jeweils für n→∞?

b) f(x)= 2-x, I=[0;2]

c) f(x)= 1/2x² I=[0;1]

d) f(x)= x² ,   I=[1;2]

e) f(x)= 2x² +1,  I=[0;2]

f) f(x)= x⁴   I=[0;2]

Comments

Berechnen sie On und Un für die Funktion f

Was ist On und Un ?

---

On= Obersumme

Un= Untersumme

---

Welcher Grenzwert ergibt sich jeweils für n→∞?

Wo kommt in den Funktionen n vor ?

---

n ist sicher die Anzahl der Teilungsintervalle ?
Ja.

---

Ich bin mir nicht sicher aber die Intervallbreite ist 2/n

---

Steht auch noch in der Aufgabe dabei, ob du neben der Betrachtung für n gegen unendlich, ober und untersumme für ein spezifisches n berechnen sollst?

---

Das sollst also zuerst die Formeln allgemein
für " n " aufstellen und dann " n " gegen
unendlich gehen lassen..

Answer 1

f(x)= 2-x, I=[0;2]

$$O_n = \sum \limits_{k=0}^{n-1}f(k \cdot \frac{2}{n})\cdot \frac{2}{n}$$

$$O_n = \sum \limits_{k=0}^{n-1}(2-k \cdot \frac{2}{n})\cdot \frac{2}{n}$$

$$O_n = \sum \limits_{k=0}^{n-1}(\frac{4}{n}-k \cdot \frac{4}{n^2})$$

$$O_n = n \cdot \frac{4}{n} - \frac{4}{n^2} \cdot \sum \limits_{k=0}^{n-1} k$$

$$O_n = 4 - \frac{4}{n^2} \cdot \frac{n \cdot (n-1) }{2} $$

$$O_n = 4 - \frac{2n^2 - 2 }{n^2} $$

Also Grenzwert 4 - 2 = 2 .   etc.

Answer 2

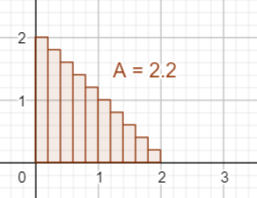
b) f(x) = 2 - x, I = [0 ; 2]

Ich mache das jetzt mal für die Obersumme

∑ (x = 1 bis n) ((b - a)/n·f(a + (b - a)/n·(x - 1)))
= ∑ (x = 1 bis n) ((2 - 0)/n·(2 - (0 + (2 - 0)/n·(x - 1))))
= ∑ (x = 1 bis n) (2/n·(2 - 2/n·(x - 1)))
= ∑ (x = 1 bis n) (4/n - 4/n^2·(x - 1))
= 4/n·n - 4/n^2·n·(n - 1)/2
= 2·(n + 1)/n
= 2 + 2/n

Der Grenzwert dürfte dann denke ich klar sein.

Schau dir das auch auf Geogebra an mit "A = Obersumme(2 - x, 0, 2, 10)"