Aufgabe:
Eine wichtige Anwendung der Ableitung einer Funktion findet sich nun bei Weg-Zeit-Funktionen \( s(t) \)
Es gelten die folgenden Zusammenhänge:
\( \begin{array}{c} \mathbf{s}^{\prime}(\mathbf{t})=\mathbf{v}(\mathbf{t}) \\ \mathbf{s}^{\prime \prime}(\mathbf{t})=\mathbf{v}^{\prime}(\mathbf{t})=\mathbf{a}(\mathbf{t}) \end{array} \)
Das bedeutet, dass die erste Ableitung der Weg-Zeit-Funktion die Momentangeschwindigkeit \( \mathrm{v}(\mathrm{t}) \) beschreibt und die zweite Ableitung die Momentanbeschleunigung a(t) eines Körpers.
Beispiel: Steinwurf.
Ein Stein werde zum Zeitpunkt \( t=0 \) s mit einer Anfangsgeschwindigkeit von \( v_{0}=20 \) \( \mathrm{m} / \mathrm{s} \) senkrecht nach oben geworfen. Bei Vernachlässigung des Luftwiderstandes gilt dann für die Flughöhe s des Steines:
\( s(t)=v_{0} \cdot t-\frac{g}{2} \cdot t^{2} \)
(Für die Erdbeschleunigung \( \mathrm{g} \) kann näherungsweise mit \( 10 \mathrm{~m} / \mathrm{s}^{2} \) gerechnet werden)
(2) Erstelle eine Wertetabelle für \( \mathrm{s}(\mathrm{t}) \) für \( 0 \leq \mathrm{t} \leq 4 \mathrm{~s} \) mit der Schrittweite \( \Delta \mathrm{t}=0,5 \mathrm{~s} \).
(5) Welche Geschwindigkeit hat der Stein 1 Sekunde nach dem Abwurf?
(6) Stelle die Funktion v(t) graphisch im Intervall [0; 4] dar.
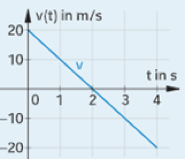
Problem/Ansatz:
Wie mache ich die Wertetabelle und was bedeut bsw v(t)