Aufgabe:
Die (normierten) Eigenvektoren und –werte können zu Matrizen zusammengefasst werden: Dazu wird die Kovarianzmatrix diagonalisiert, d.h. man berechnet eine Matrix. Okay in Sigma stehen auf der Diagonalen die Eigenwerte. Mir geht es jetzt speziell um die orthonormale Matrix.

Text erkannt:
\( \Sigma=\left(\begin{array}{cccc}\lambda_{1} & 0 & \ldots & 0 \\ 0 & \lambda_{2} & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \ldots & 0 & \lambda_{d}\end{array}\right) \in \mathbb{R}^{d \times d} \)
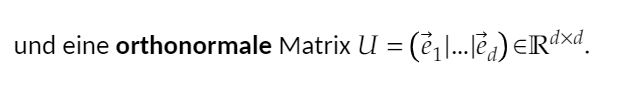
Wenn wir z. B. die beiden Eigenvektoren haben.
Text erkannt:
und eine orthonormale Matrix \( U=\left(\vec{e}_{1}|\ldots| \vec{e}_{d}\right) \in \mathbb{R}^{d \times d} \).
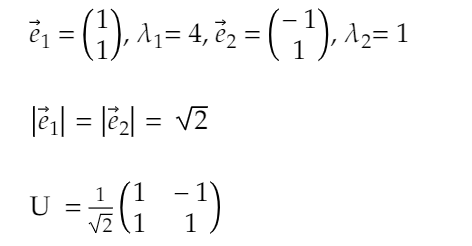
Text erkannt:
\( \vec{e}_{1}=\left(\begin{array}{c}1 \\ 1\end{array}\right), \lambda_{1}=4, \vec{e}_{2}=\left(\begin{array}{c}-1 \\ 1\end{array}\right), \lambda_{2}=1 \)
\( \left|\vec{e}_{1}\right|=\left|\vec{e}_{2}\right|=\sqrt{2} \)
\( \mathrm{U}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1 & -1 \\ 1 & 1\end{array}\right) \)
Problem/Ansatz:
Was ich hierbei jetzt nicht verstehe ist, beide Eigenvektoren haben die Länge Wurzel 2 also kann ich diese mit 1 / Wurzel 2 normieren und in die Matrix schreiben.
Was wäre aber, wenn meine Eigenvektoren (1 1) und (3 1) wären? Dann muss ich beide ja unterschiedliche normieren. Wie würde man das in diesem Fall machen? ich kann ja nicht einfach beide Faktoren vor die Matrix schreiben. Hängt das irgendwie mit dem Begriff orthonormale Matrix zu tun? Dass dabei irgendetwas gegeben sein muss?