Aufgabe:
Die Zeit X (in Tagen), die ein Arbeitsloser braucht, um wieder eine Anstellung zu finden, hat annähernd eine Wahrscheinlichkeitsverteilung mit folgender Dichtefunktion:
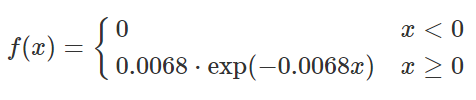
Text erkannt:
\( f(x)=\left\{\begin{array}{ll}0 & x<0 \\ 0.0068 \cdot \exp (-0.0068 x) & x \geq 0\end{array}\right. \)
a. Wie groß ist die Wahrscheinlichkeit, dass ein Arbeitsloser genau 309 Tage benötigt, um eine Anstellung zu finden? (Geben Sie das Ergebnis in Prozent an.)
b. Wie groß ist die Wahrscheinlichkeit, dass ein Arbeitsloser zwischen 118 und 156 Tage benötigt, um eine Anstellung zu finden? (Geben Sie das Ergebnis in Prozent an.)
c. Nach wie vielen Tagen hat ein Arbeitsloser mit einer Wahrscheinlichkeit von 69% eine Anstellung gefunden?
d. Wie viele Tage dauert es im Mittel, bis ein Arbeitsloser wieder eine Anstellung findet?
Problem/Ansatz:
Hallo, leider weiß ich nicht wie ich auf die Verteilungsfunktion komme, um die weiteren Aufgaben zu lösen. Außerdem stehe ich bei den Fragen c. und d. auf der Leitung. Wäre schön, wenn mir jemand helfen könnte. LG