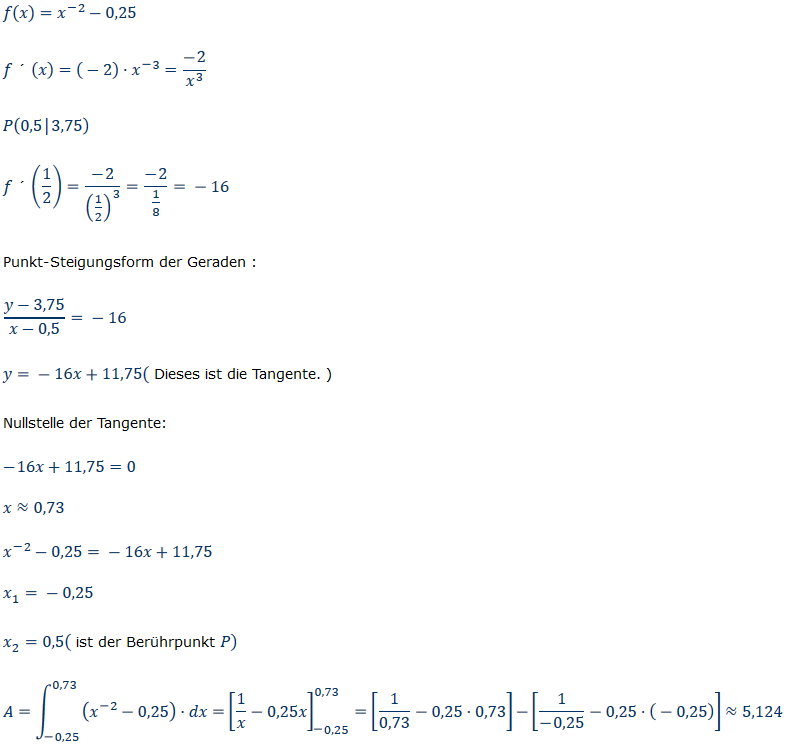
Text erkannt:
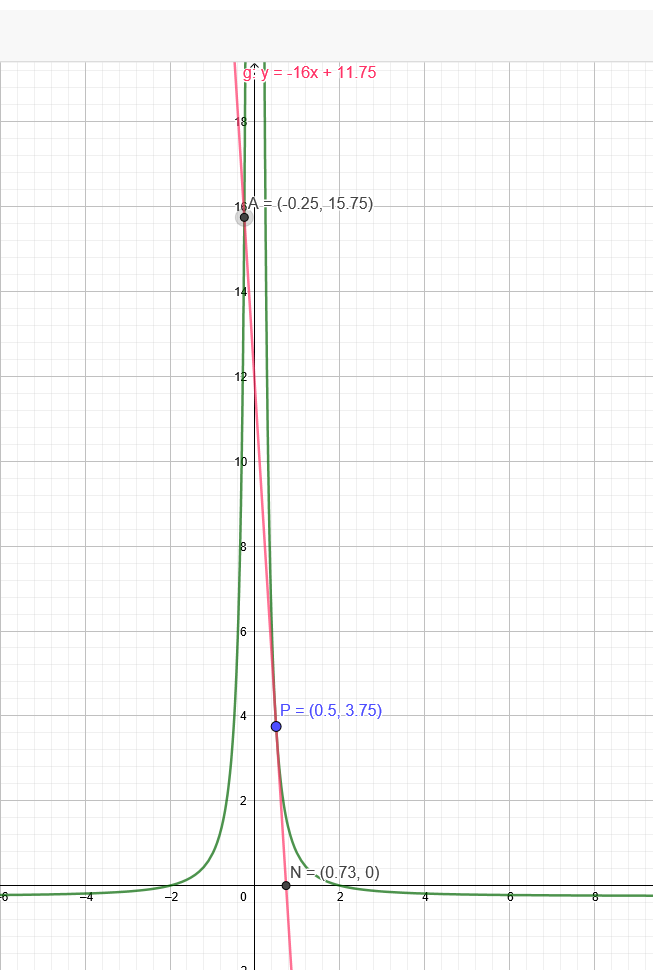
\( f(x)=x^{-2}-0,25 \)
\( f \cdot(x)=(-2) \cdot x^{-3}=\frac{-2}{x^{3}} \)
\( P(0,5 \mid 3,75) \)
\( f \cdot\left(\frac{1}{2}\right)=\frac{-2}{\left(\frac{1}{2}\right)^{3}}=\frac{-2}{\frac{1}{8}}=-16 \)
Punkt-Steigungsform der Geraden :
\( \frac{y-3,75}{x-0,5}=-16 \)
\( y=-16 x+11,75( \) Dieses ist die Tangente. \( ) \)
Nullstelle der Tangente:
\( -16 x+11,75=0 \)
\( x \approx 0,73 \)
\( x^{-2}-0,25=-16 x+11,75 \)
\( x_{1}=-0,25 \)
\( x_{2}=0,5 \) ( ist der Berührpunkt \( \left.P\right) \)
\( A=\int \limits_{-0,25}^{0,73}\left(x^{-2}-0,25\right) \cdot d x=\left[\frac{1}{x}-0,25 x\right]_{-0,25}^{0,73}=\left[\frac{1}{0,73}-0,25 \cdot 0,73\right]-\left[\frac{1}{-0,25}-0,25 \cdot(-0,25)\right] \approx 5,124 \)