Ausgangsfunktion bilden, muss durch Punkt P gehen

Question

Aufgabe:

Aufgangfunktion bilden deren Graph durch. Punkt P verläuft

Problem/Ansatz:

F‘(x)=-7x^-8-3x^-4.   //P(1/2)

Ausgangsfunktion

F(x)= x^-7-x^-3+c

Einsetzen P

2= 1^-7-1^-3+c

C=2

F(x)=1^-7-1^-3+2

Richtig???

Answer 1

F '(x)=-7x^-8-3x^-4. Dann ist F(x)=x^-7+x^-3+c.

P einsetzen: 2=1+1+c oder c=0.

F(x)=x^-7+x^-3.

Answer 2

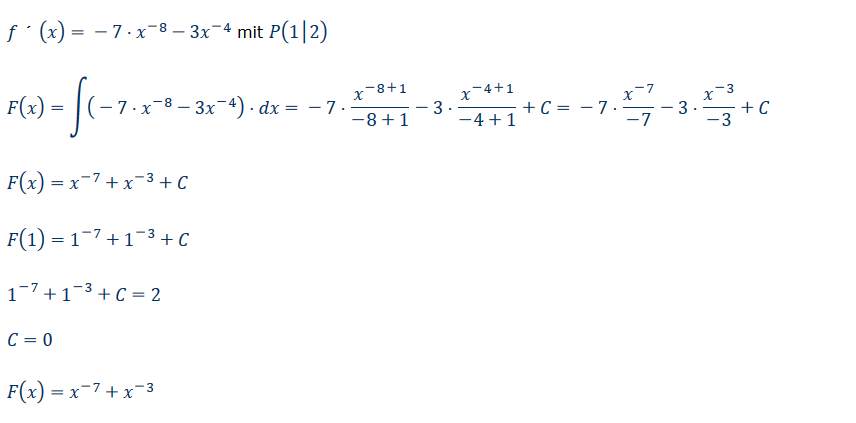
Text erkannt:

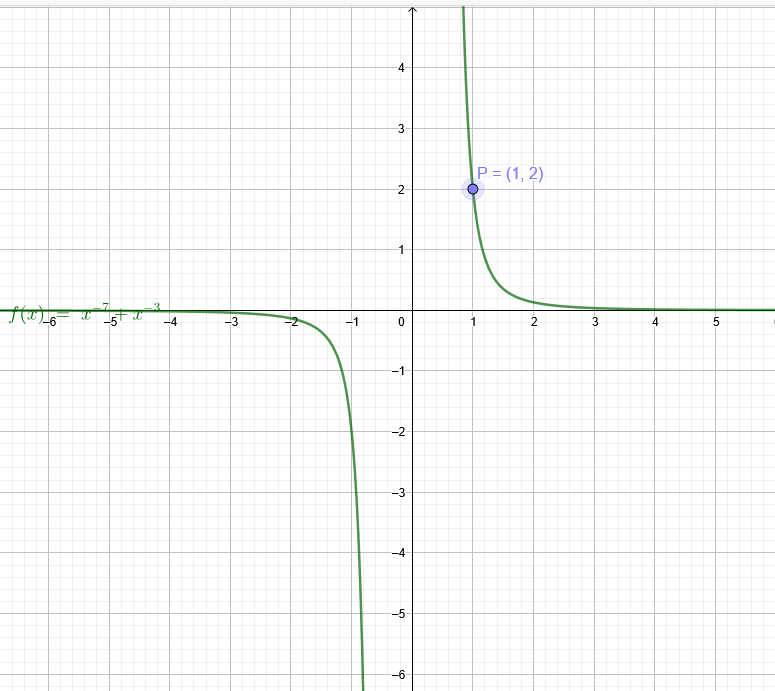
$f \cdot(x)=-7 \cdot x^{-8}-3 x^{-4}$ mit $P(1 \mid 2)$
$F(x)=\int\left(-7 \cdot x^{-8}-3 x^{-4}\right) \cdot d x=-7 \cdot \frac{x^{-8+1}}{-8+1}-3 \cdot \frac{x^{-4+1}}{-4+1}+C=-7 \cdot \frac{x^{-7}}{-7}-3 \cdot \frac{x^{-3}}{-3}+C$
$F(x)=x^{-7}+x^{-3}+C$
$F(1)=1^{-7}+1^{-3}+C$
$1^{-7}+1^{-3}+C=2$
$C=0$
$F(x)=x^{-7}+x^{-3}$