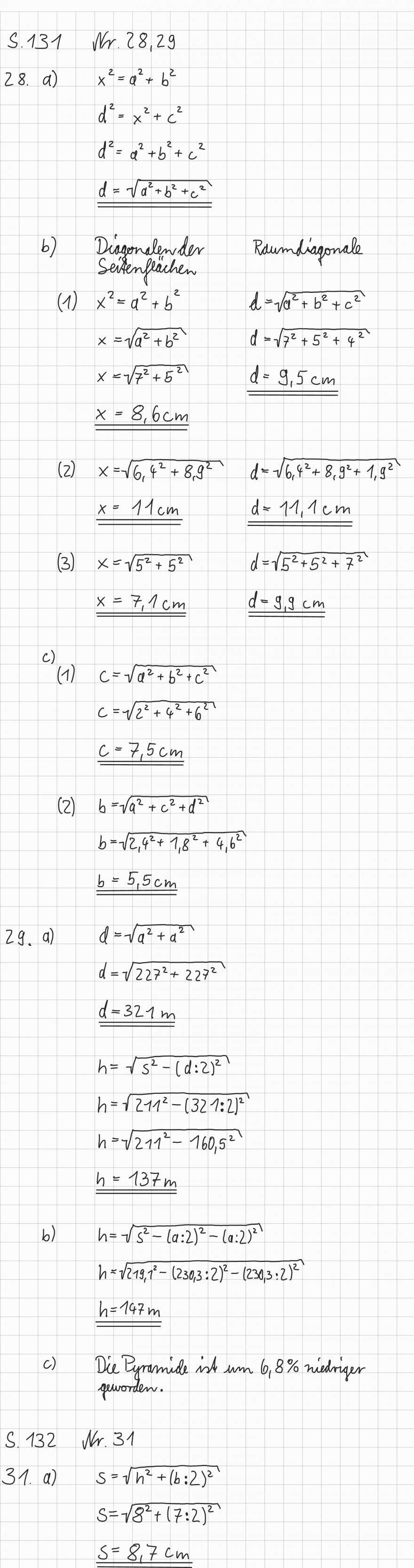
Text erkannt:
5.131 Nr. 28,29
28. a) \( x^{2}=a^{2}+b^{2} \)
\( d^{2}=x^{2}+c^{2} \)
\( d^{2}=a^{2}+b^{2}+c^{2} \)
\( d=\sqrt{a^{2}+b^{2}+c^{2}} \)
b) Dicgenalender Rdumbiagonale Serienfecchen
(1) \( x^{2}=a^{2}+b^{2} \quad d=\sqrt{a^{2}+b^{2}+c^{2}} \)
\( x=\sqrt{a^{2}+b^{2}} \quad d=\sqrt{7^{2}+5^{2}+4^{2}} \)
\( x=\sqrt{7^{2}+5^{2}} \quad d=9,5 \mathrm{~cm} \)
\( x=8,6 \mathrm{~cm} \)
(2) \( \quad x=\sqrt{6,4^{2}+8,9^{2}} \quad d=\sqrt{6,4^{2}+8,9^{2}+1,9^{2}} \)
\( x=11 \mathrm{~cm} \quad d=11,1 \mathrm{~cm} \)
(3) \( \quad x=\sqrt{5^{2}+5^{2}} \quad d=\sqrt{5^{2}+5^{2}+7^{2}} \)
\( x=7,1 \mathrm{~cm} \)
\( d=g, 9 \mathrm{~cm} \)
c)
(1) \( c=\sqrt{a^{2}+b^{2}+c^{2}} \)
\( c=\sqrt{2^{2}+4^{2}+6^{2}} \)
\( c=7,5 \mathrm{~cm} \)
(2) \( \quad b=\sqrt{a^{2}+c^{2}+d^{2}} \)
\( b=\sqrt{2,4^{2}+1,8^{2}+4,6^{2}} \)
\( \underline{b}=5,5 \mathrm{~cm} \)
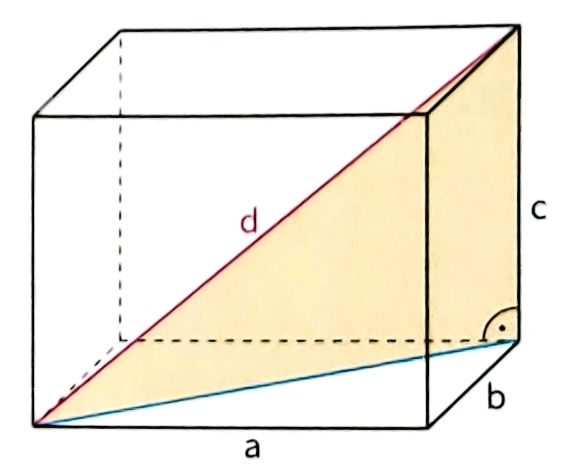
29. a) \( \quad d=\sqrt{a^{2}+a^{2}} \)
\( d=\sqrt{227^{2}+227^{2}} \)
\( d=321 \mathrm{~m} \)
\( h=\sqrt{s^{2}-(d: 2)^{2}} \)
\( h=\sqrt{211^{2}-(321: 2)^{2}} \)
\( h=\sqrt{211^{2}-160,5^{2}} \)
\( n=137 \mathrm{~m} \)
b) \( \quad h=\sqrt{s^{2}-(a: 2)^{2}-(a: 2)^{2}} \)
\( h=\sqrt{219,1^{2}-(230,3: 2)^{2}-(230,3: 2)^{2}} \)
\( \underline{h=147 \mathrm{~m}} \)
c) Die Pyramide ist un \( 6,8 \% \) nidriger quorten
S.132 \( \mathrm{kr} .31 \)
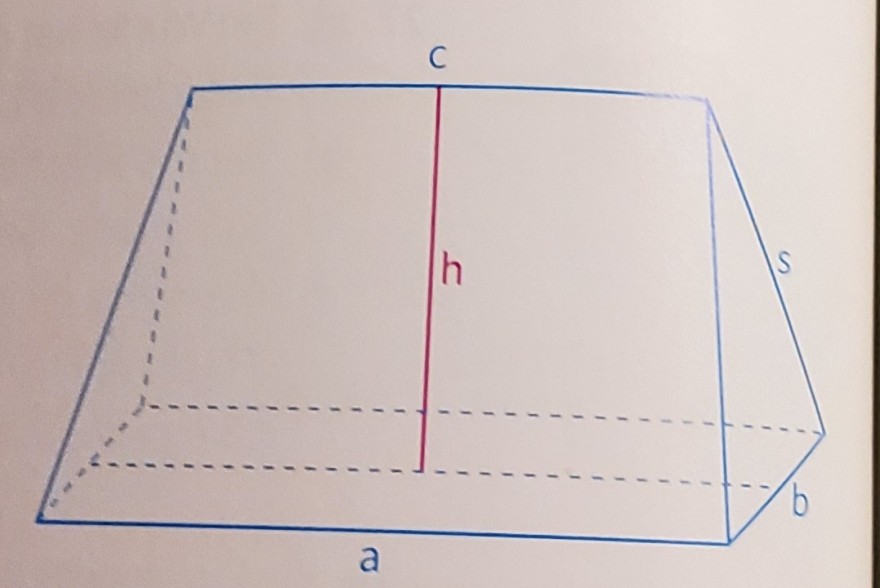
31. a) \( \quad s=\sqrt{h^{2}+(b: 2)^{2}} \)
\( S=\sqrt{8^{2}+(7: 2)^{2}} \)
\( s=8,7 \mathrm{~cm} \)
Zu 28.
Text erkannt:
\( Z \)
Zu 29.
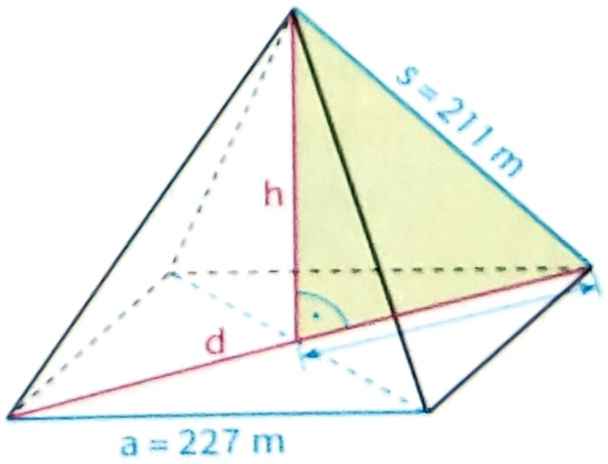
Zu 31.