Rekonstruktion / Funktionsfindung: zum Ursprung punktsymmetrisch

Question

Aufgabe:

Der Graph einer zum Ursprung punktsymmetrischen ganzrationalen Funktion 5. Grades hat den Sattelpunkt Ws(1/8).

Problem/Ansatz:

Wie löst man diese Aufgabe?

Answer 1

Wegen der Ursprungssysmmetrie hat die Funktion die Form f(x)=ax^5+cx^3+e*x.

Du kennst f(1), f'(1) und f''(1).

Drei Unbekannte und drei Gleichungen dafür - du musst das System nur noch lösen.

Comments

Wie löst man ungefähr das System?

Und danke

---

Gegenfrage: Wie lauten die 3 Gleichungen des Gleichungssystems?

Answer 2

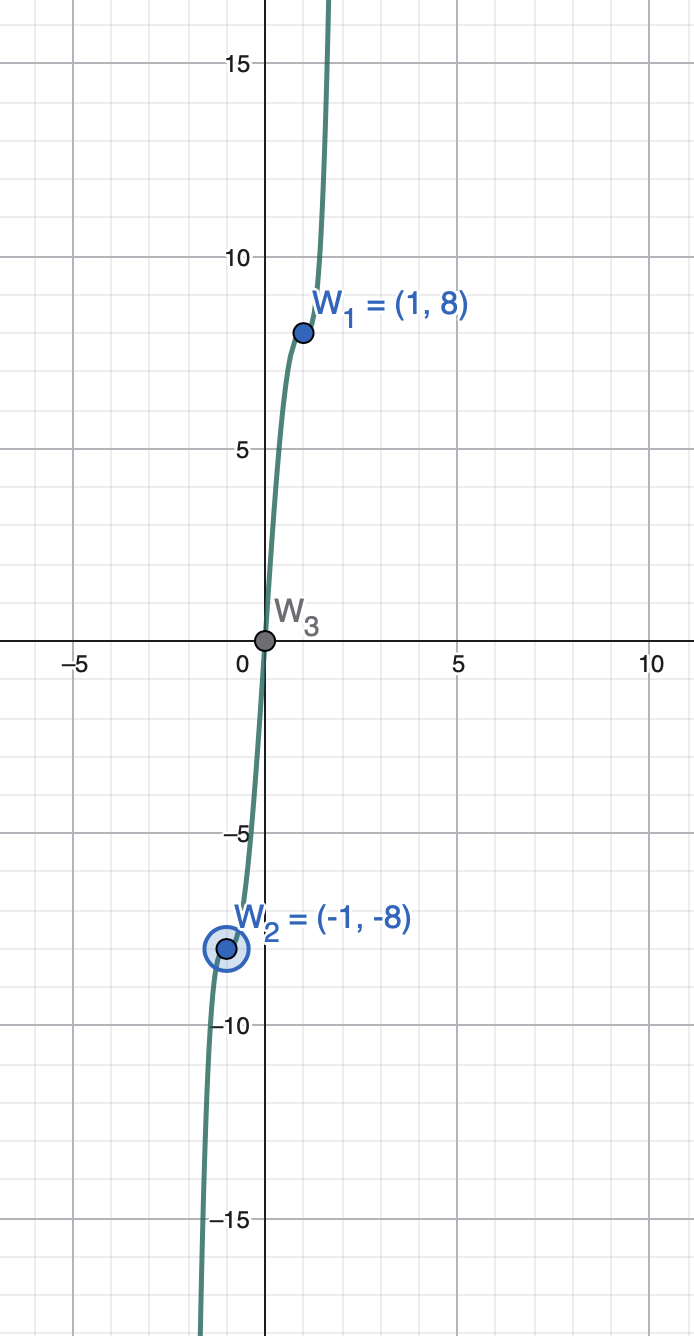
Der Graph einer zum Ursprung punktsymmetrischen ganzrationalen Funktion 5. Grades hat den Sattelpunkt \( W_s(1|8)\)

Allgemein:    \(f(x)=ax^5+bx^4+cx^3+dx^2+ex +f \)

Punktsymmetrie erfordert ungerade Potenzen:

\(f(x)=ax^5+cx^3+ex  \)  

\(f(1)=a+c+e \)

1.)   \(a+c+e=8  \)

Wendepunkt  2.Ableitung.

\(f'(x)=5ax^4+3cx^2+e \)

\(f''(x)=20ax^3+6cx \)

\(f''(1)=20a+6c \)   

2.)

\(20a+6c=0 \)

Beim Sattelpunkt ist eine waagerechte Tangente: 1.Ableitung

\(f'(1)=5a+3c+e \).

3.)

\(5a+3c+e =0\) Löse nun das System mit dem Mittel deiner Wahl.

Ich erhalte:

\( a=3 \)    \( c=-10 \)und  \( e=15 \)

\(f(x)=3x^5-10x^3+15x \)