1.) Motivation.
Man hat von einem Sachverhalt Messdaten der Form \((x_0,y_0),...,(x_l,y_l)\in \mathbb{R}^2\) gegeben und will diese nun mit einem Polynom \(p\) minimalsten Grades interpolieren, d.h dieses gesuchte Polynom geht durch all diese Messpunkte. Jetzt interessiert man sich für eine Stelle \(x\) zwischen den Messstellen für den Funktionswert \(p(x)\).
Nun bekommt man noch weitere Messdaten \((x_{l+1},y_{l+1}),...,(x_r,y_r)\in \mathbb{R}^2\) hinzu, welche auch interpoliert werden sollen, um mit dem Polynom genauere Vorhersagen dazwischen treffen zu können, zb wieder an derselben Stelle \(x\).
Vielleicht ahnt man schon das Problem: Man muss das Interpolationspolynom komplett neu berechnen, obwohl man sich doch nur für Werte zwischen den Messpunkten interessiert.
Beispielsweise hat man \(500+1=501\) Messpunkte gegeben. Also lautet das Interpolationspolynom vom Grundansatz
$$ \begin{aligned} p_{500}(x)=a_0+a_1x^1+...+a_{499}\cdot x^{499}+a_{500}\cdot x^{500} \end{aligned} $$
Man erhält also ein lineares Gleichungssystem mit \(501\) Gleichungen und Unbekannten \(a_0,a_1,...,a_{500}\). Das zu lösen ist mit sehr viel Aufwand verbunden. Der Aufwand liegt hier in der Ordnung von \(\mathcal{O}(n^3)\); mit \(n=501\) im wesentlichen also \(501^3=125.751.501\) Aufwandsschritte, wenn man einmal von Zwischenrechnungen beim Lösen absieht. Wenn nun aber nochmals \(100\) weitere Messdaten hinzukommen, wird der Aufwand in der Größenordnung von \(601^3=217.081.801\) liegen. Das Alles nur, um wenige Zwischenstellen zu berechnen?
Es wäre doch viel einfacher, die Werte zwischen den Messwerten berechnen zu können, ohne das Interpolationspolynom explizit gegeben haben zu müssen. Die gute Nachricht ist, dass das der sogenannte Neville-Aitken-Algorithmus ermöglicht. Dieser soll nun intuitiv hergeleitet werden.
2.) Abstraktion des obigen Problems.
Es seien \(n+1\) verschiedene Stützpunkte der Form \((x_0,y_0),...,(x_n,y_n)\in \mathbb{R}^2\) gegeben, wobei \(x_0<x_1<...<x_n\) vorausgesetzt wird. Gesucht ist nun das Interpolationspolynom \(p\in \mathbb{R}[x]\) vom Grad \(\deg(p)=n\) für diese Stützpunkte, sodass \(p(x_i)=y_i\) für alle \(i=0,...,n\) gilt.
Nun sei eine weitere Stelle \(t\in [x_0,x_n]\setminus\{x_0,...,x_n\}\) gegeben. Das Interpolationspolynom \(p\) soll an dieser Stelle \(t\) ausgewertet werden.
3.) Naive Konstruktion durch Rekursion.
Betrachte wieder die oben genannten Stützpunkte \((x_0,y_0),...,(x_n,y_n)\in \mathbb{R}^2\) mit \(x_0<x_1<...<x_n\). Nun sei angenommen, dass für die Stützpunkte \((x_0,y_0),...,(x_{n-1},y_{n-1})\in \mathbb{R}^2\) das Interpolationspolynom \(q\) und für die Stützpunkte \((x_1,y_1),...,(x_n,y_n)\in \mathbb{R}^2\) das Interpolationspolynom \(r\) gegeben ist. Dann gilt jeweils:
\(q(x_i)=y_i\) für alle \(i=0,...,n-1\) und
\(r(x_k)=y_k\) für alle \(k=1,...,n\).
Beide Polynome haben den Grad \(n-1\). Definiere nun damit folgende Funktion:
\(p(x):=\frac{q(x)\cdot (x-x_n)-r(x)\cdot (x-x_0)}{x_0-x_n}\).
Dies ist eine Polynomfunktion vom Grad \(n\) und erfüllt alle \(n+1\) Interpolationsbedingungen. Es gilt nämlich:
\(p(x_0)=\frac{q(x_0)\cdot (x_0-x_n)-r(x_0)\cdot (x_0-x_0)}{x_0-x_n}=\frac{q(x_0)\cdot (x_0-x_n)}{x_0-x_n}=q(x_0)=y_0\),
\(p(x_n)=\frac{q(x_n)\cdot (x_n-x_n)-r(x_n)\cdot (x_n-x_0)}{x_0-x_n}=\frac{-r(x_n)\cdot (x_n-x_0)}{x_0-x_n}=r(x_n)=y_n\)
und für alle \(j=1,...,n-1\) hat man
\(\begin{aligned} p(x_j)&=\frac{q(x_j)\cdot (x_j-x_n)-r(x_j)\cdot (x_j-x_0)}{x_0-x_n}\\[10pt]&=\frac{y_j\cdot (x_j-x_n)-y_j\cdot (x_j-x_0)}{x_0-x_n}\\[10pt]&=\frac{y_j\cdot x_j-y_j\cdot x_n-y_j\cdot x_j+y_j\cdot x_0}{x_0-x_n}\\[10pt]&=\frac{-y_j\cdot x_n+y_j\cdot x_0}{x_0-x_n}\\[10pt]&=\frac{y_j\cdot (x_0-x_n)}{x_0-x_n}=y_j. \end{aligned}\)
Also erfüllt die Funktion $$ p(x)=\frac{q(x)\cdot (x-x_n)-r(x)\cdot (x-x_0)}{x_0-x_n} $$ alle \(n+1\) Interpolationsbedingungen.
4.) Algorithmische Umsetzung.
4.1) Aufwandsabschätzung.
Betrachten wir nun mal die Funktion $$ p(x)=\frac{q(x)\cdot (x-x_n)-r(x)\cdot (x-x_0)}{x_0-x_n} $$ von Abschnitt 3.) genauer und setzen uns mit dem Rechenaufwand auseinander. Beispielsweise hat man für \(n=4\) also \(4+1=5\) Messpunkte
\((x_0,y_0),(x_1,y_1),(x_2,y_2),(x_3,y_3),(x_4,y_4)\in \mathbb{R}^2\).
Für eine Auswertung von \(p\) an einer Stelle \(t\) zwischen diesen Messstellen muss also nun folgendes berechnet werden:
\(p(t)=\frac{q(t)\cdot (x-x_n)-r(t)\cdot (x-x_0)}{x_0-x_n}\).
Dafür muss aber schon der Wert
\(q(t)=\frac{l(t)\cdot (x-x_n)-w(t)\cdot (x-x_0)}{x_0-x_n}\) und der Wert
\(r(t)=\frac{f(t)\cdot (x-x_n)-s(t)\cdot (x-x_0)}{x_0-x_n}\)
bekannt sein, wobei jeweils die Funktionen \(l,w,f,s\) Funktionen (analog zu \(q\) und \(r\) mit Grad um eins weniger)sind, dessen Wert ja auch schon bekannt sein muss. Diese Rekursion lässt sich folgendermaßen veranschaulichen:
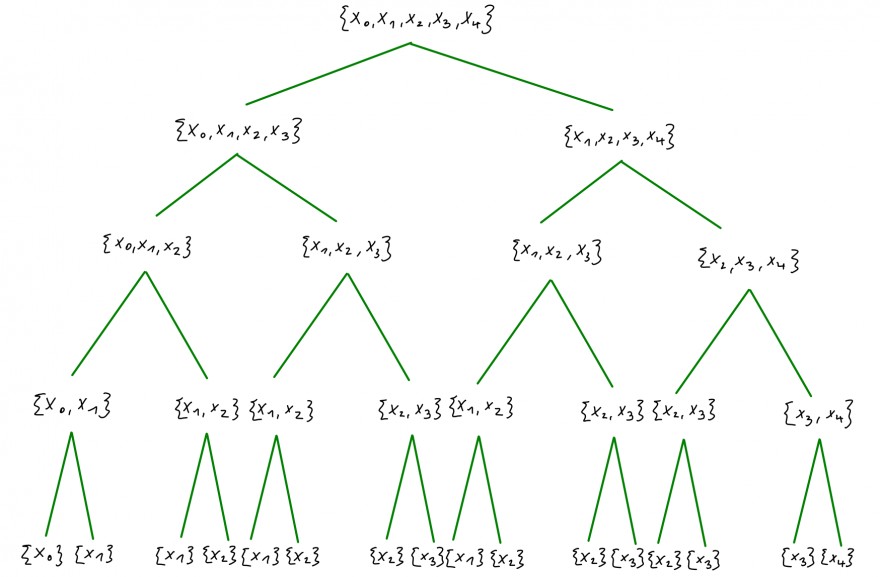
Jeder Knoten dieses Baumes visualisiert, welche Stützstellen \(x_i\) bereits in die Berechnung eingeflossen sind. Die Blätter unten deuten demnach die Messstellen an, welche vorgegeben sind. In diesem Baum wird bei genauem Hinsehen deutlich, dass der naive Ansatz der obigen Konstruktion zu einem exponentiellen Auswuchs der Rekursionen führt, weil Funktionswerte unnötigerweise mehrmals abgefragt werden. Konkret hat man hier für \(n=4\) also \(2^0+2^1+2^2+2^3+2^4=31\) einzelne Aufrufe. Weitet man dies nun für beliebiges \(n\in \mathbb{N}\) aus, so hat man einen Aufwand von \(\Theta(2^n)\) zu erwarten, denn pro Stockwerk verdoppeln sich die Rekursionsaufrufe und man erhält:
\(\sum\limits_{i=0}^n 2^i=\frac{1-2^{n+1}}{1-2}=2^{n+1}-1\in \Theta(2^n)\).
Selbst für einen leistungsstarken Rechner ist dieser Aufwand nicht mehr vertretbar! Der nächste Bereich beschäftigt sich nun mit der Frage, wie dieses Verfahren beschleunigt werden kann.
4.2) Verbesserung.
Nach obigem Beispiel empfiehlt es sich also, Redundanzen aus dem Baum zu entfernen:
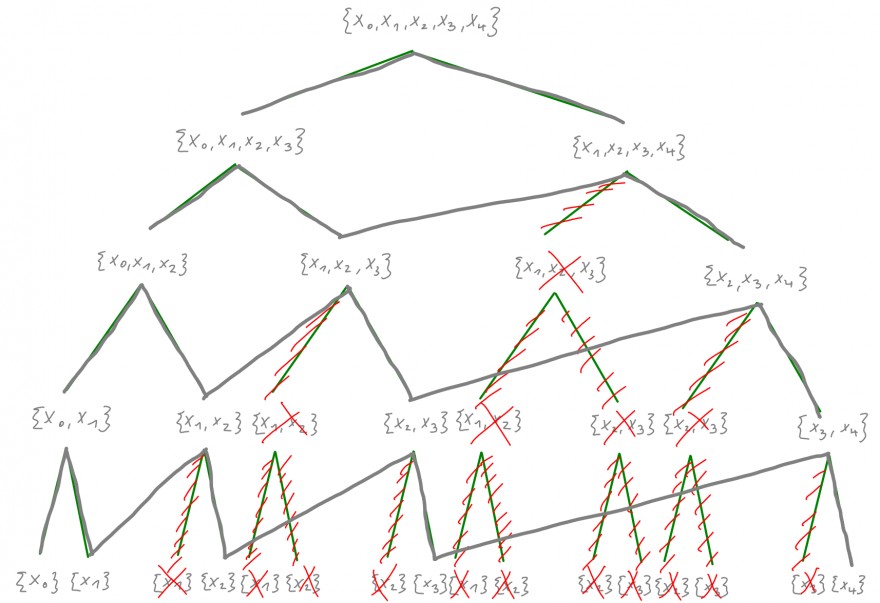
Hierbei werden nun alle Redundanzen rot markiert und die grauen Einfärbungen beschreiben die neuen Pfade:

Die Anzahl der Aufrufe erhöht sich also nur noch linear und man erhält nur noch einen Aufwand von \(\Theta(n^2)\), denn
\(\sum\limits_{i=0}^n i=\frac{n(n+1)}{2}=\frac{n^2+n}{2}\in \Theta(n^2)\).
Statt also \(31\) Aufrufe machen zu müssen, sind also nur noch \(25\) notwendig. Bei \(n=10\) wird der Unterschied noch deutlicher. Folgende rot -und blaufarbige Markierungen im Graph deuten nun die Arbeitsweise an, wie die Berechnungen angestellt werden, was dem Neville-Aitken-Algorithmus entspricht:
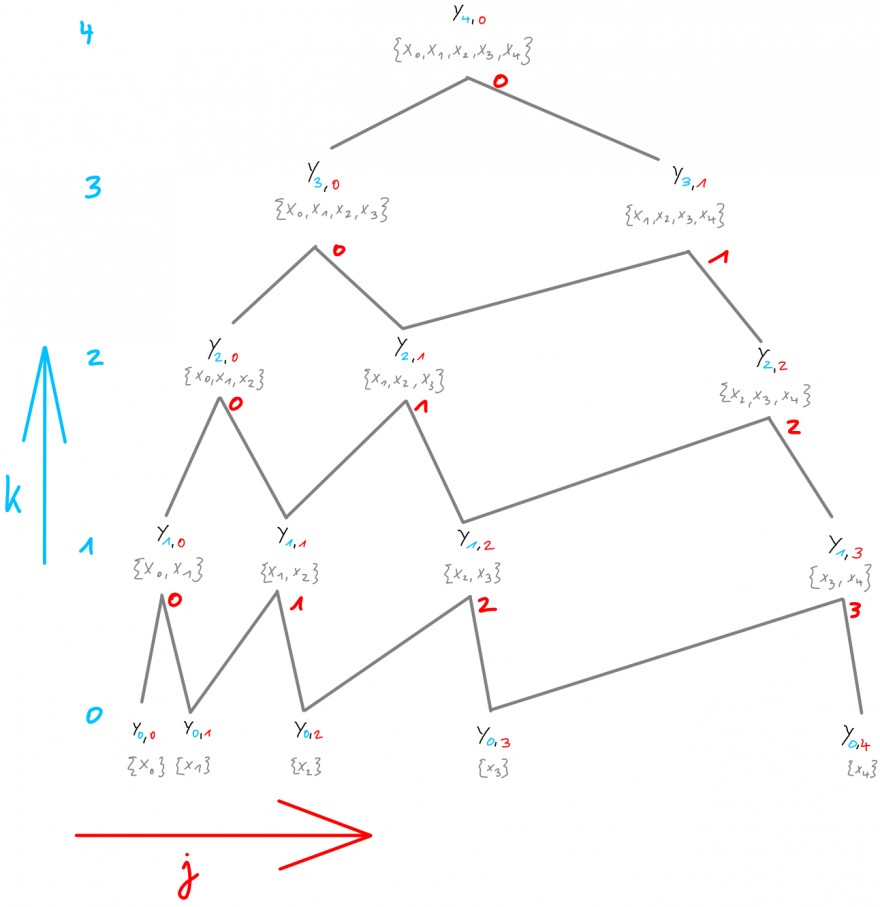
Allgemein gilt für alle \(k=1,...,n\) und für alle \(j=0,...,n-k\)
\(\begin{aligned}\qquad \qquad y_{k,j}=\frac{y_{k-1,j}\cdot (x-x_{k+j})-y_{k-1,j+1}\cdot (x-x_j)}{x_j-x_{k+j}}\end{aligned}\).
Ab hier klar machen, dass diese Formel als Analogie aus
\(p(t)=\frac{q(t)\cdot (t-x_n)-r(t)\cdot (t-x_0)}{x_0-x_n}\)
von 3.) folgt. Demnach wird auffallen, dass
\(p(t)=\frac{q(t)\cdot (t-x_n)-r(t)\cdot (t-x_0)}{x_0-x_n}=y_{n,0}\)
gilt.
4.3) Pseudo-Code.
Dieses verbesserte Verfahren kann nun zu folgenden Pseudo-Code verdichtet werden:
\(\begin{aligned}\text{Setze } y_0&:=y_{0,0}\\y_1&:=y_{1,0}\\&\vdots \\y_n&:=y_{n,0}\end{aligned}\)
Eingabe: Listen \(X:=[x_0,...,x_n],Y:=[y_0,...y_n]\in \mathbb{R}\) und Auswertungsstelle \(t\in \mathbb{R}\)
Ausgabe: Wert des Interpolationspolynoms \(p(t)\)
Algorithmus:
Initialisiere \(X=[x_0,...,x_n],\quad Y=[y_0,...y_n],\quad t\)
Für \(k=1,...,n\) berechne:
__Für \(j=0,...,n-k\) berechne:
____Setze \(Y[j] \leftarrow \frac{Y[j]\cdot (t-x_{k+j})-Y[j+1]\cdot (t-x_j)}{x_j-x_{k+j}}\)
Ausgabe \(Y[0]\)
Dabei bezeichnet \(Y[j]\) den \(j\)-ten Eintrag der Liste von \(Y\).
5.) Fazit.
Der Neville-Aitken-Algorithmus eignet sich vorallem dann, wenn man sehr viele Messpunkte gegeben hat und das dazugehörige Interpolationspolynom nur an wenigen ausgewählten Stellen auswerten möchte. Es können dabei beliebig viele Punkte hinzugefügt werden, ohne das Interpolationspolynom explizit ausrechnen zu müssen.
Im folgendem Kommentar ist ein Beispiel vorgerechnet zu finden.