Körperberechnung Analytische Geometrie

Question

könnte mir jemand bei diesen Aufgaben helfen bzw. erklären wie ich diese lösen soll mit Rechenwegen? Es muss nicht der Lösung entsprechen..

Die quadratische und ebene Grundfläche eines Körpers hat die Eckpunkte A1(4|4|0), A2(4|–4|0), A3(–4|–4|0), A4(–4|4|0),
Die Deckfläche dieses Körpers ist ebenfalls eben und hat die Eckpunkte B1(2|3|4), B2(3|–2|4), B3(–2|–3|4), B4(–3|2|4)

Punkte mit gleichem Index sind mit einer geradlinigen Strecke verbunden. Damit entsteht ein „verdrehter Pyramidenstumpf“.

a) Zeichnen sie eine Aufsicht auf den Körper („in der x3-Richtung nach unten auf die x1-x2-Ebene blickend“) und überzeugen Sie sich davon, dass auch die Deck- fläche dieses Körpers ein Quadrat ist!
b) Welche Länge haben die Seitenkanten s des Körpers?
c) Begründen Sie, dass die Seitenflächen des Körpers nicht eben sind! (Tipp: „eben“ kommt von „Ebene“!)
d) Begründen Sie mit einer Rechnung, dass sich die Verlängerungen der Seiten- kanten (z. B. die durch die Strecke A1B1 und die Strecke A3B3 bestimmten Geraden) nicht schneiden!
e) Um welchen Winkel sind die Seitenkanten gegen die Horizontalebene geneigt?

Vielen Dank..

Answer 1

Hallo,

a) Zeichnen sie eine Aufsicht auf den Körper („in der x3-Richtung nach unten auf die x1-x2-Ebene blickend“) und überzeugen Sie sich davon, dass auch die Deck- fläche dieses Körpers ein Quadrat ist!

D.h. Du schaust von oben auf die verdrehte Pyramide drauf:

Das Viereck $B_1B_2B_3B_4$ ist augenscheinlich ein Quadrat.

b) Welche Länge haben die Seitenkanten s des Körpers?

Die Länge einer Seitenkante ist$$|A_1B_1| = |B_1 - A_1| = \left| \begin{pmatrix}2\\ 3\\ 4\end{pmatrix} - \begin{pmatrix}4\\ 4\\ 0\end{pmatrix} \right| \\ \phantom{|A_1B_1|} = \left| \begin{pmatrix}-2\\ -1\\ 4\end{pmatrix}\right| = \sqrt{(-2)^2+(-1)^2 + 4^2} \\ \phantom{|A_1B_1|} = \sqrt{21}$$mache das gleiche mit den anderen Seitenkanten, das Ergebnis ist immer das selbe.

c) Begründen Sie, dass die Seitenflächen des Körpers nicht eben sind! (Tipp: „eben“ kommt von „Ebene“!)

Die vier Eckpunkte einer Seitenfläche (z.B. $A_1A_2B_2B_1$) liegen nicht in einer Ebene.

d) Begründen Sie mit einer Rechnung, dass sich die Verlängerungen der Seiten- kanten (z. B. die durch die Strecke A1B1 und die Strecke A3B3 bestimmten Geraden) nicht schneiden!

Erstelle für zwei der Seitenkanten die Geradengleichung ...$$g_1: \quad \vec x = A_1 + s(B_1 - A_1) = \begin{pmatrix}4\\ 4\\ 0\end{pmatrix} + s \begin{pmatrix}-2\\ -1\\ 4\end{pmatrix} \\ g_3: \quad \vec x = A_3 + s(B_3 -A_3) = \begin{pmatrix}-4\\ -4\\ 0\end{pmatrix} + t \begin{pmatrix}2\\ 1\\ 4\end{pmatrix}$$... und versuche den Schnittpunkt zu berechnen$$\begin{aligned} g_1 &= g_3 \\ \begin{pmatrix}4\\ 4\\ 0\end{pmatrix} + s \begin{pmatrix}-2\\ -1\\ 4\end{pmatrix} &= \begin{pmatrix}-4\\ -4\\ 0\end{pmatrix} + t\begin{pmatrix}2\\ 1\\ 4\end{pmatrix}\\ s \begin{pmatrix}-2\\ -1\\ 4\end{pmatrix} + t \begin{pmatrix}-2\\ -1\\ -4\end{pmatrix} &= \begin{pmatrix} -8\\ -8\\ 0\end{pmatrix} \end{aligned}$$Das sind drei Gleichungen für die zwei Unbekannten $s$ und $t$. Multipliziere die zweite Gleichung mit 2 und ziehe sie von der ersten ab. Dann steht dort $0=8$. Das ist bereits ein Widerspruch Es existiert also kein Paar $(s, \,t)$ welches die drei Gleichungen erfüllt.

Daraus folgt: die Geraden $g_1$ und $g_2$ haben keinen gemeinsamen Schnittpunkt.

e) Um welchen Winkel sind die Seitenkanten gegen die Horizontalebene geneigt?

Sei $\alpha$ der Winkel der Seitenkante $\vec{A_1B_1}$ zur Senkrechten $e_z$ so ist $$\cos(\alpha) = \frac{\vec{A_1B_1} \cdot e_z}{|\vec{A_1B_1}| \cdot |e_z|} = \frac{4}{\sqrt{21}} \implies \alpha \approx 29,2°$$Der Winkel $\varphi$ der Seitenkante $A_1B_1$ zur Horizontalebene ist dann$$\varphi = 90° - \alpha \approx 60,8°$$

Den Winkel zur Kontrolle in Geoknecht3D eingegeben ...

Comments

Vielen Dank für deine hilfreiche Antwort!

---

hilfreich wäre es, wenn Du konkrete Fragen stellst ;-)

Answer 2

Du könntest Deine Angaben hier

https://www.geogebra.org/m/jukhtjp4

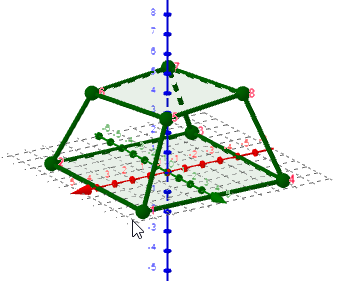
verarbeiten, um eine Ansicht/Graph zu haben (den Schrägbildaspekt musst du nicht beachten)

z.B.

Figure:{(4, 4, 0), (4, -4, 0), (-4, -4, 0), (-4, 4, 0), (2, 3, 4), (3, -2, 4), (-2, -3, 4), (-3, 2, 4)}

Grid:{{1, 2, 3, 4}, {5, 6, 7, 8}, {1, 5}, {4, 8}, {3, 7}, {2, 6}}

Comments

Wie genau soll ich das auf ein Koordinatensystem mit x und y zeichnen?

---

Du sollst den Schrägbildaspekt nicht beachten, sondern die o.g. Daten eingeben, um das 3D Bild zu haben. Wenn Deine Daten in Figure und Grid stehen, dann kannst Du das Fenster schließen.

Vielleicht auch genauere Fragen stellen?