Berechnen Sie anhand eines Punktes, eines Winkel und einer Länge die Start- und Endkoordinaten einer Linie, und die …

Question

Aufgabe:

Berechnen Sie anhand eines Punktes, eines Winkel und einer Länge die Start- und Endkoordinaten einer Linie, und die Koordinaten einer dazu senkrechten Linie der gleichen Länge, deren Mittelpunkt den Endkoordinaten der ersten Linie entspricht..

Problem/Ansatz:

Die Berechnung der Endkoordinaten der ersten Linie habe ich wie folgt gemacht:

x1 = länge * cos(pi * winkel/ 180.0);

y1 = länge * sin(pi * winkel/ 180.0);

Aber wie genau soll ich die Koordinaten einer dazu senkrechten Linie berechnen? Hier eine Grafik zur Veranschaulichung der Fragestellung (Abstand zwischen grüner und gelber Linie soll vernachlässigt werden):

Text erkannt:

$\frac{m}{1}$

Comments

Aber wie genau soll ich die Koordinaten einer dazu senkrechten Linie berechnen?

Da gibt's unendlich viele Möglichkeiten. Gibt es irgendeine Aussage zur Positionierung der gelben Strecke?

Falls nicht, was spricht dagegen, $(x_4|\,y_4)=(x_0|\,y_0)$ zu setzen ?

---

Stimmt, das hab ich leider total vergessen, ich werde das gleich zur Frage hinzufügen. Der Mittelpunkt der grünen Linie soll die Koordinaten (x2|y2) haben.

Answer 1

Hallo,

Ich habe die Aufgabe so verstanden, dass ein Punkt $P_1$, ein Winkel $\alpha$ und eine Länge $a$ gegeben ist.

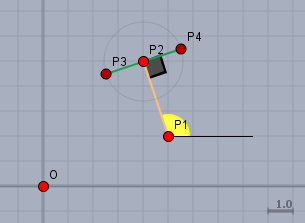
Nun sollen die drei Punkte $P_2$, $P_3$ und $P_4$ berechnet werden, so dass der eingezeichnete gelbe Winkel $=\alpha$, die Strecke $|P_1P_2|=|P_3P_4|=a$, $P_2$ der Mittelpunkt der Strecke $|P_3P_4|$ und der Winkel $\angle P_1P_2P_4$ ein rechter ist.

Da geht so. Stelle folgende drei Punkte auf:$$Q_2 = \begin{pmatrix}a\\ 0\end{pmatrix}, \quad Q_3= \begin{pmatrix}a\\ a/2\end{pmatrix}, \quad Q_4 = \begin{pmatrix}a\\ -a/2\end{pmatrix}$$Sowie die Drehmatrix $D$$$D = \begin{pmatrix}\cos \alpha& -\sin \alpha\\ \sin \alpha& \cos \alpha\end{pmatrix}$$und berechne jeden der drei Punkte $P_i$ nach folgender Vorschrift:$$P_i = D \cdot Q_i + P_1, \quad i=\{2,3,4\}$$

Nachtrag: Ohne die Schreibweise mit Matrizen-Vektor-Multiplikation geht es so: stelle zwei Vektoren auf:$$u = a \cdot \begin{pmatrix}\cos \alpha\\ \sin \alpha\end{pmatrix}= \begin{pmatrix}a \cos \alpha\\ a \sin \alpha\end{pmatrix} \\ v = \frac a2 \cdot \begin{pmatrix} -\sin \alpha \\ \cos \alpha \end{pmatrix} = \begin{pmatrix} -\frac a2\sin \alpha \\ \frac a2\cos \alpha \end{pmatrix}$$Die beiden Vektoren stehen senkrecht auf einander. Die Punkte $P_{2,3,4}$ berechnen sich dann nach$$P_2 = P_ 1 + u \\ P_3 = P_2 + v \\ P_4 = P_2 - v$$Ob Du Punkt oder Vektor hast, macht hier bei der Rechnung keinen Unterschied. Die eigentliche nummerische Rechnung ist identisch mit der Variante oben, aber in der Matrix-Vektor-Form ist die Schreibweise kompakter.

Comments

Die Aufgabenstellung hast du vollkommen richtig verstanden. Vielen Dank für deine Antwort, auch wenn ich davon maximal die Hälfte verstanden habe. Von Matrizen- und Vektormultiplikation habe ich nämlich keinen blassen Schimmer :D

---

kannst Du Vektoren aufstellen und addieren und subtrahieren?

---

Ja, das kriege ich hin.

---

Ok - ich habe die Antwort dahingehend (hoffentlich) verständlicher formuliert.

---

Vielen Dank!

---

Könntest du mir bitte bei meiner aktuellen Frage helfen?

Weiß nicht, wie man mit 3 y Werten umgeht, sonst nur Aufgaben mit mehreren x-Werten gelöst.

Wäre nett, wenn du mir weiterhelfen könntest :)