es geht um die Lösungsmenge einer Ungleichung

Question

Aufgabe: -1/(x+1)²< -100 für alle xeR

Problem/Ansatz: Da das eine Ungleichung ist und mir aktuell die Übung damit fehlt, sind es hier die Minuszeichen, weswegen ich hier nicht weiterkomme.

Answer 1

Wenn du beide Seiten mit der negativen Zahl (-1) multiplizierst, dreht sich das Relationszeichen um:

1/(x+1)²>100

Das gilt aber NICHT für alle xeR, sondern nur für (x+1)²<0,01.

Comments

0<(x+1)²<0,01

Da fehlt noch etwas.

Answer 2

- 1/(x + 1)² < -100
- 1 < -100·(x + 1)²
- 1/(-100) > (x + 1)²
1/100 > (x + 1)²
(x + 1)² < 1/100
-1/10 < x + 1 < 1/10
-11/10 < x < -9/10

Comments

Könntest Du mir bitte die Vorzeichen bei den jeweiligen Umformungen erklären und warum ist bei der dritten Umformung die -100 in Klammern gesetzt. Im Voraus schon Mal Danke.

Answer 3

$\frac{1}{(x+1)^2}$ >100|*$\frac{(x+1)^2}{100}$

(x+1)^2<$\frac{1}{100}$|$\sqrt{}$

1.) x+1<$\frac{1}{10}$

x₁<-1+$\frac{1}{10}$=-0,9

2.) x+1>-$\frac{1}{10}$

x₂>-1-$\frac{1}{10}$=-1,1

-1,1<x<-0,9

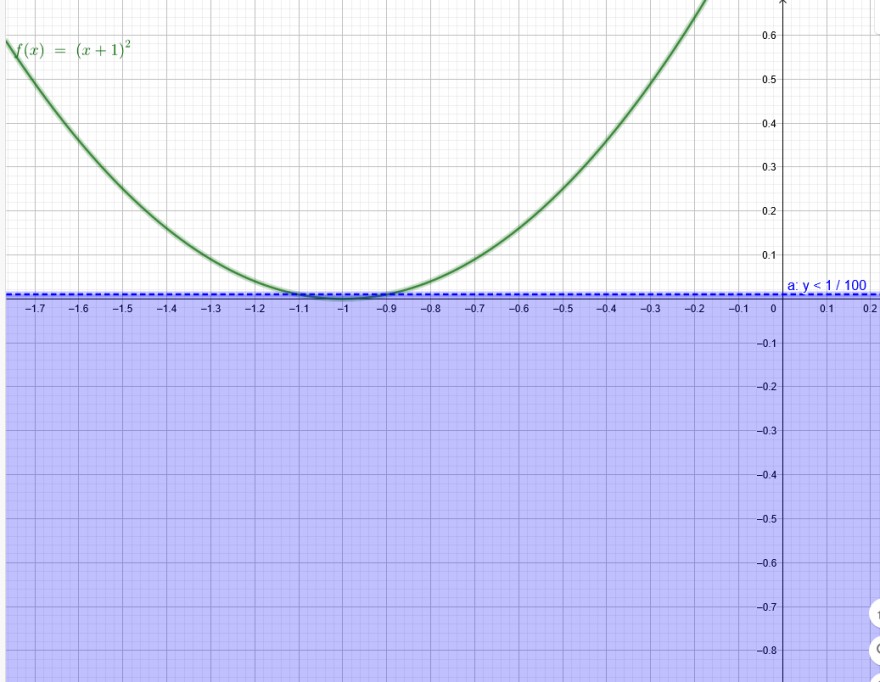
$\frac{1}{(x+1)^2}$ >100

Wolfram bringt folgendes als Ergebnis:

(-1,1<x<1)

(-1<x<-0,9)

Somit musst du die Polstelle bei x=-1 auch beachten.

Answer 4

-1/(x+1)²< -100

x=-1 ist verboten, da der Nenner dann gleich Null wäre.

Mit -1 multiplizieren, Kleiner → Größer

1/(x+1)²>100     |*Nenner  |:100

Da der Nenner nicht negativ sein kann, ändert sich das Größer-Zeichen nicht.

1/100>(x+1)²

|x+1|<0,1

-0,1<x+1<0,1     |-1

-1,1<x<-0,9

Da x≠-1 sein muss, ist die Lösung

-1,1<x<-1 oder -1<x<-0,9