Matrix Drehachse, Drehwinkel, Element in SO(3)

Question

Aufgabe:

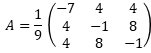
Text erkannt:

\( A=\frac{1}{9}\left(\begin{array}{ccc}-7 & 4 & 4 \\ 4 & -1 & 8 \\ 4 & 8 & -1\end{array}\right) \)

 1) Zeige das A Element in SO(3) ist.

 2) Bestimme Drehachse und Drehwinkel

Problem/Ansatz:

a) wie zeigt man das A in Element SO(3) ist?

b) was ist SO(3) einfach erklärt?

c) Wie bestimmt man bei einer Matrix den Drehwinkel? Was hat das 1/9 vor der Matrix für einen Effekt?

d) Wenn man den Drehachse hat, wie kommt man dann auf den Drehwinkel?

Folgendes habe ich schon errechnet:

Determinante von A = 729

Eigenwerte x1 = 9 und x2 = -9

Eigenvektoren:

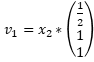
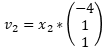
Text erkannt:

\( v_{2}=x_{2} *\left(\begin{array}{c}-4 \\ 1 \\ 1\end{array}\right) \)

würde mich freuen wenn jemand das Vorgehen am Lösungsweg erklären könnte.

VG coffee.cup

Answer 1

Aloha :)

Die Gruppe der speziellen orthogonalen Transformationen im \(\mathbb R^3\), kurz \(SO(3)\), beschreibt Drehungen im 3-dimensionalen Raum, bei denen die Längen von Vektoren und die Winkel, die von zwei Vektoren eingeschlossen werden, ungeändert bleiben. Unter solchen Transformationen ändert sich ein 3-dimensionales Volumen nicht und auch die Orientierung der Vektoren zueinander bleibt erhalten. Formal drückt sich das darin aus, dass die Determinante einer Matrix \(A\in SO(3)\) gleich \(1\) ist.

Wir prüfen das nach:

$$\operatorname{det}A=\frac19\left|\begin{array}{rrr}-7 & 4 & 4\\4 & -1 & 8\\4 & 8 & -1\end{array}\right|=\frac19\left|\begin{array}{rrr}-7 & 4 & 4\\4 & -1 & 8\\0 & 9 & -9\end{array}\right|=\left|\begin{array}{rrr}-7 & 4 & 4\\4 & -1 & 8\\0 & 1 & -1\end{array}\right|$$$$\phantom{\operatorname{det}A}=\left|\begin{array}{rrr}-7 & 8 & 4\\4 & 7 & 8\\0 & 0 & -1\end{array}\right|=-(-49-32)=81\ne1$$

Das heißt \(A\not\in SO(3)\).

Comments

danke für die Antwort :)

Kann man in dem Fall dann keine Drehachse / Drehwinkel berechnen?

---

Die Drehachse ist der Eigenvektor zum Eigenwert \(1\). Diesen Eigenwert gibt es bei dieser Matrix aber nicht.

---

Okay,

kennst du vielleicht eine Matrix welche man Drehachse und Drehwinkel berechnen kann, an dem du das vorrechnen/erklären kannst?

---

\(\color{blue}\det A=\dfrac19\left\lvert\begin{array}{rrr}-7&4&4\\4&-1&8\\4&8&-1\end{array}\right\rvert\)  scheint mir schon falsch zu sein.

Richtig scheint mir  \(\det A=\dfrac1{9^3}\left\lvert\begin{array}{rrr}-7&4&4\\4&-1&8\\4&8&-1\end{array}\right\rvert=1\).

---

okay, also muss die Matrix sozusagen zu 1 "normiert" werden?

Muss ich bei den Eigenvektoren die 1/9³ beachten? oder hätte ich dann die selben Eigenvektoren?

Muss dann die Matrix aus den Eigenwerten gebildet werden und sieht so aus?

Text erkannt:

\( D=\left(\begin{array}{ccc}-1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1\end{array}\right) \)

Weiter ginge es mit den Matrizen in der Form, welche ich die nehmen muss welche die 1 an der selben Position gibt (es gibt ja 3 von denen für x y z)

Text erkannt:

\( M=\left(\begin{array}{ccc}\cos \phi & -\sin \phi & 0 \\ \sin \phi & \cos \phi & 0 \\ 0 & 0 & 1\end{array}\right) \)

dazu muss ich aber sagen das die Reihenfolge der EW in D vertauscht werden können, oder ist da eine Reihenfolge? ansonsten wäre die Matrix M ja eine andere wenn die 1 an anderer Stelle stehen würde. Aber mir fällt auf das das Ergebnis des Winkels in allen 3 Fällen der Reihenfolge gleich ist. oder muss ich für die Positionen der Sinuswerte die Ursprungsmatrix nehmen

---

ich hab zu einer vermutlich parallel laufenden frage

https://www.mathelounge.de/871619/bestimmen-drehwinkel-und-drehachse-der-folgenden-matrix-a#c871632

ein paar hinweise gegeben. interessant ist erstmal der eigenwert 1 und der dazu gehörende eigenvektor - der drehachse. die matrix einer drehung um koordinaten achsen die du angegeben hast ist was anderes als die matrix einer drehung um eine beliebige ursprungs gerade. herleitung siehe https://www.geogebra.org/m/NXx4E8cb#material/fdmmvvma

diese matrix könnte man durch hintereinander ausführen von drehungen um die koordinatenachsen zusammen setzen

---

Der Vektor \(v=\begin{pmatrix}1\\2\\2\end{pmatrix}\) ist ein Eigenvektor zum Eigenwert \(\lambda=1\) der Matrix \(A\). Drehachse ist der normierte Eigenvektor, also \(\frac1{\lVert v\rVert}v=\frac13\cdot\begin{pmatrix}1\\2\\2\end{pmatrix}\). Für den Drehwinkel \(\varphi\) gilt
\(\cos(\varphi)=\frac12\big(\operatorname{Spur}(A)-1\big)=\frac12(-1-1)=-1\), also \(\varphi=\pm\pi\).
Quelle: https://vhm.mathematik.uni-stuttgart.de/Vorlesungen/Lineare_Algebra/Folien_Drehachse_und_Drehwinkel.pdf.