Parkettierung mit Dreilingen

Question

Welches ist das kleinste Rechteck, das aus einer ungeraden Anzahl von Einheitsquadraten besteht und vollständig mit L-Dreilingen aus drei Einheitsquadraten

parkettiert werden kann?

Answer 1

Hallo Roland,

[spoiler]

Das gesuchte Rechteck habe die Seitenlängen \(a\) und \(b\). Da es aus einer ungeraden Anzahl von Einheitsquadraten bestehen soll, müssen \(a\) und \(b\) ebenfalls beide ungerade sein. Da mindestens ein L-Dreiling enthalten ist, müssen beide Seiten größer als 1 sein. Zusammen folgt daraus$$a\ge 3 \land b \ge 3$$Wenn eine Seite die Länge 3 hat, so ist die einzig möglich Anordnung für die L-Drillingen an dieser Seite:

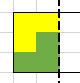
Das bedeutet aber, dass rechts von dieser Anordnung ein weiteres kleineres Rechteck existiert, welches den Anforderungen genügt. Diese zwei L-Drillinge lassen sich also entfernen und wenn man sich dann die beiden nächsten L-Drillinge an der neu entstandenen Seite anschaut, lässt sich dies unendlich fortsetzen.

Daraus folgt: eine Seitenlänge von 3 ist nicht möglich!

Weiter muss mindestens eine Seitenlänge durch 3 teilbar sein, da die Gesamtfläche durch 3 teilbar ist. Somit ist die nächst kleinere Kombination$$5 \times 9$$und hier lässt sich ein Rechteck finden:

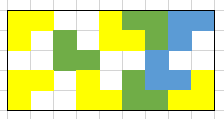
Also ist ein Rechteck der Seitenlängen \(5 \times 9\) das kleinst mögliche.

[/spoiler]

Comments

@Werner: Wie immer von dir: Eine ausgezeichnete Antwort.